Касательная к окружности

Наши курсы по подготовке к ЕГЭ по математике, информатике и физике

К ЕГЭ можно подготовиться . У нас на сайте полно качественных материалов. Но вы должны знать что вы делаете. 

• У вас должен быть план, чтобы вы шли от простого к сложному и не «захлебнулись». 
• Вас должен кто-то проверять и указывать короткий путь, чтобы вы не теряли время.
• Вас должен кто-то мотивировать, чтобы вы не бросили все.

Если у вас с этим сложности, приходите к нам.

• Начните с нашего гида о том как подготовиться к ЕГЭ по математике.
• Посетите наши бесплатные вебинары по математике, информатике и физике.

И если вам нужен действительно высокий балл, приходите на наши курсы: 

• Подготовка к ЕГЭ по математике
• Подготовка к ЕГЭ по информатике
• Подготовка к ЕГЭ по физике

Ход занятия:

Новый материал:

Рубрика «Это интересно!»

С незапамятных времен человек использовал в своей жизни простейшие геометрические построения. Одним из таких построений является деление окружности на равные части. Примеров можно привести много. Превращение колеса из сплошного диска в обод со спицами поставило человека перед необходимостью распределить спицы в колесе равномерно.

С делением окружности неразрывно связано построение правильных многоугольников. Правильные многоугольники встречаются в древнейших орнаментах у всех народов.

В декоративно- прикладном искусстве дизайнеры, ювелиры и представители многих других профессий с успехом применяли деление окружности, создавая прекрасные произведения. Это ордена, медали, монеты и ювелирные украшения.

Орден Красной Звезды Орден Отечественной войны

Самым распространенным примером применение деления окружности на равные части является создание логотипов, эмблем, товарных знаков различных фирм. Иногда достаточно увидеть эмблему на капоте или крыле автомобиля и безошибочно назвать марку.

Показ наглядных пособий использования геометрических построений в строительстве, архитектуре, машиностроении, а также природные явления.

Построение круга, окружности.

Круг – это часть плоскости, ограниченная окружностью.

Окружность – замкнутая плоская кривая, все точки которой равноудалены от центра.

Чтобы изобразить круг, достаточно взять блюдце или тарелку и обвести.

Для построения окружности необходимо найти центр. Из центра циркулем провести окружность.

Этапы построения:

1. Начертить квадрат.
2. Разделить стороны квадрата на две равные части, отметить буквами или цифрами.
3. Через полученные точки провести центровую линию (штрихпунктирную) Сначала горизонтальную, затем вертикальную.
4. Пересечение линий отметить точкой О – центр окружности.
5. В точку О поставить ножку циркуля и начертить окружность. Центр окружности является также и центром круга.

Запомнить: в центре должны обязательно пересекаться штрихи, проведенных центровых (осевых) линий, а не точки. В окружностях меньших размеров допускается проводить вместо штрихпунктирных линий тонкие линии построения.

Для построения окружностей и кругов используют трафареты.

Демонстрация, показ.

Деление окружности на равные части.

Любая прямая, проведенная через центр окружности, делит эту окружность на две равные части. Две взаимно перпендикулярные прямые, проведенные через центр окружности, делят эту окружность на 4 равные части.

Окружность можно разделить на 8 равных частей, используя линейку или угольники.

Демонстрация, показ.

Если соединить, полученные при делении точки окружности, то мы получим правильные многоугольники.

При делении окружности на 3, 6, 12 равных частей используют не только угольники, но и циркуль. В результате построения можно увидеть правильный равносторонний треугольник, правильный шестиугольник (рисунок 5)

Демонстрация, показ.

Закрепление:

Фрагмент из рабочей тетради.

Приготовь для работы циркуль, карандаш с маркировкой Т и ТМ, линейку, трафарет. Все построения выполняй аккуратно.

Используя трафарет с окружностями, изобрази круг.

Для построения окружности необходимо провести штрихпунктирные линии. Эти линии состоят из штриха и точки. При пересечении они образуют центр окружности и являются центровыми или осевыми линиями.

Установи ножку циркуля в центре пересечения осевых (центровых) линий и проведи окружность.

Этапы построения окружности:

1. Начертить квадрат.
2. Разделить все стороны квадрата на две равные части, отметить полученные точки.
3. Через точки провести центровую линию (штрихпунктирную) карандашом с маркировкой Т. Сначала горизонтальную, затем вертикальную.
4. Пересечение линий отметить точкой О – центр окружности.
5. В точку О поставить ножку циркуля и начертить окружность.

Центр окружности является также и центром круга.

Первый метод определения радиуса дуги или сегмента круга

Изначально это выглядит так:

Рисунок 463.1. а) имеющаяся дуга, б) определение длины хорды сегмента и высоты.

Таким образом, когда имеется дуга, мы можем соединить ее концы и получим хорду длиной L. Посредине хорды мы можем провести линию, перпендикулярную хорде и таким образом получим высоту сегмента H. Теперь, зная длину хорды и высоту сегмента, мы можем сначала определить центральный угол α, т.е. угол между радиусами, проведенными из начала и конца сегмента (на рисунке 463.1 не показаны), а затем и радиус окружности.

Решение подобной задачи достаточно подробно рассматривалось в статье «Расчет арочной перемычки», поэтому здесь лишь приведу основные формулы:

tg(a/4) = 2Н/L (278.1.2)

тогда

а/4 = arctg(2H/L)

R = H/(1 — cos(a/2)) (278.1.3)

Как видим, с точки зрения математики никаких проблем с определением радиуса окружности нет. Данный метод позволяет определить значение радиуса дуги с любой возможной точностью. Это главное достоинство данного метода.

А теперь поговорим о недостатках.

Проблема данного метода даже не в том, что требуется помнить формулы из школьного курса геометрии, успешно забытые много лет назад — для того, чтобы напомнить формулы — есть интернет. А вот калькулятор с функцией arctg, arcsin и проч. есть далеко не у каждого пользователя. И хотя эту проблему также успешно позволяет решить интернет, но при этом не следует забывать, что мы решаем достаточно прикладную задачу. Т.е. далеко не всегда нужно определить радиус окружности с точностью до 0.0001 мм, точность 1 мм может быть вполне приемлема.

Кроме того, для того, чтобы найти центр окружности, нужно продлить высоту сегмента и отложить на этой прямой расстояние, равное радиусу. Так как на практике мы имеем дело с не идеальными измерительными приборами, к этому следует прибавить возможную погрешность при разметке, то получается, что чем меньше высота сегмента по отношению к длине хорды, тем больше может набежать погрешность при определении центра дуги.

Опять же не следует забывать о том, что мы рассматриваем не идеальный случай, т.е. это мы так сходу назвали кривую дугой. В действительности это может быть кривая, описываемая достаточно сложной математической зависимостью. А потому найденный таким образом радиус и центр окружности могут и не совпадать с фактическим центром.

В связи с этим я хочу предложить еще один способ определения радиуса окружности, которым сам часто пользуюсь, потому что этим способом определить радиус окружности намного быстрее и проще, хотя точность при этом значительно меньше.

Как нарисовать ровный круг без помощи циркуля

Вы можете быть школьником, который пришел на урок геометрии, забыв инструменты для черчения, студентом, взрослым человеком, вынужденным начертить идеально ровную окружность, — ситуации случаются разные.

Каждому человеку полезно будет знать, как нарисовать ровный круг без циркуля. Мы предлагаем вам несколько способов решения данной задачи.

Заменить циркуль легко может другой инструмент, находящийся в пенале у каждого школьника, а именно – транспортир. Положите его на бумагу, отметив центральную точку на прямой части, это будет центр будущего круга. Обведите внутреннюю часть полукруга, затем поверните линейку примерно на девяносто градусов и дорисуйте треть круга. Поверните транспортир еще раз и завершите круг.

Если вы находитесь на совещании или на рабочем месте, но под рукой не оказалось нужного инструмента, просто воспользуйтесь компакт-диском. Обведите его с внешней стороны или с внутренней для получения фигуры меньшего размера.

В офисной обстановке можно также воспользоваться стаканом. Для этого возьмите стакан с водой, сделайте глоток и поставьте на лист бумаги, легким движением обведите дно. Попейте еще и отставьте его в сторону.

Все вышеперечисленные предметы можно найти в любом офисе, транспортир будет доступен и ученикам. С помощью них вы сможете ровно нарисовать круг без циркуля.

Основные характеристики окружности

1. Радиус — это отрезок, соединяющий центр с какой-либо точкой окружности. У любой окружности можно провести бесконечно много радиусов, которые будут иметь одну и ту же длину. Обозначают радиус r или R. На Рис.2 представлена окружность с центром в точке О радиусом ОА.

2. Хорда — это отрезок, соединяющий две точки окружности. У любой окружности можно провести бесконечно много хорд. На Рис.3 ВС и KD — хорды окружности с центром в точке О.

3. Диаметр — это отрезок, соединяющий две точки окружности и проходящий через ее центр (т.е. диаметр — это частный случай хорды). У любой окружности можно провести бесконечно много диаметров, которые будут иметь одну и ту же длину. На Рис.4 МN — диаметр окружности с центром в точке О. Обозначают диаметр d или D. Диаметр в два раза больше радиуса, т.е. d = 2r (D = 2R), откуда r = d : 2 (R = D : 2), следовательно, центр окружности (точка О) является серединой диаметра.

4. Дуга — это часть окружности, ограниченная двумя точками. На Рис.5 KDC и KBC — дуги, ограниченные точками К и С.

Измерение углов

Центральные углы. Углы, имеющие вершину при центре, называются центральными углами.

Относительно этих углов имеют место следующие теоремы.

Теорема 74. Равным центральным углам в одной и той же окружности соответствуют равные дуги.

Дано. Углы AOB и COD равны (черт. 109).

Требуется доказать, что ◡AB = ◡CD.

Доказательство. Проведем хорды AB и CD и соединим точки A, B, C, D с центром. Два треугольника AOB и COD равны, ибо AO = CO и BO = DO как радиусы, ∠AOB = ∠COD по условию. Следовательно, хорды AB и CD равны.

Против равных хорд лежат равные дуги, следовательно и дуги AB и CD равны: ◡AB = ◡CD (ЧТД).

Теорема 75 (обратная 74). Равным дугам в одной и той же окружности соответствуют равные углы.

Дано. Дуги AB и CD равны (черт. 109).

Требуется доказать, что ∠AOB = ∠COD.

Доказательство. Из того, что дуги AB и CD равны, следует, что и хорды AB и CD тоже равны (теорема 61).

Два треугольника AOB и COD равны, ибо AB = CD как равные хорды, AO = CO и BO = DO как радиусы. Следовательно, ∠AOB = ∠COD (ЧТД).

Теорема 76. Отношение центральных углов равно отношению соответствующих им дуг.

Даны два центральные угла AOB и COD (черт. 110).

Требуется доказать, что

AOB/COD = AB/CD.

Доказательство. Здесь имеют место два случая:

1) Когда дуги AB и CD соизмеримы и 2) когда они несоизмеримы.

1-й случай. Дуги AB и CD соизмеримы.

Пусть дуга AE будет их общей мерой. Положим, что она p раз содержится в дуге AB и q раз в дуге CD. Разделив дугу AB на p, а CD на q равных частей и соединив точки деления дуг с центром O, мы разделим угол AOB на p, а угол COD на q равных углов, из которых каждый равен углу AOE.

Из равенств

AB = pAE, CD = qAE
AOB = pAOE, COD = qAOE

получаем

AOB/COD = p/q, AB/CD = p/q, откуда
AOB/COD = AB/CD (ЧТД).

2-й случай. Дуги AB и CD несоизмеримы.

Отложим дугу AF равную CD и соединим F с O. Углы AOF и COD равны.

Требуется доказать, что

AOB/AOF = AB/AF

Доказательство. A) Положим

AOB/AOF > AB/AF (1).

Для того, чтобы имело место равенство, нужно дробь во второй части неравенства (1) увеличить. Для этого следует ее знаменатель уменьшить.

Положим, мы нашли, что имеет место равенство

AOB/AOF = AB/AG (a)

Разделим дугу AB на равное число таких частей, чтобы каждая часть была менее GF; тогда одна из точек деления i упадет в промежутке между G и F. Дуги AB и Ai соизмеримы, следовательно,

AOB/AOi = AB/Ai (b).

Разделив равенства (b) на (a), находим

AOF/AOi = AG/Ai

равенство несообразное, ибо первая часть его больше, а вторая меньше 1, следовательно, допущение (1) не имеет места.

B) Допустим, что

AOB/AOF < AB/AF (2)

Тогда вторую часть этого неравенства нужно уменьшить для того, чтобы имело место равенство. Для этого нужно знаменатель дроби AB/AF увеличить. Положим, мы нашли такую точку H, чтобы удовлетворялось равенство

AOB/AOF = AB/AH (c)

Разделив дугу AB на такие равные части, чтобы каждая часть была меньше FH, мы найдем, что одна из точек деления J упадет в промежуток между F и H. Дуги AB и AJ будут соизмеримы, следовательно,

AOB/AOJ = AB/AJ (d)

Разделив равенство (d) на (c) найдем

AOF/AOJ = AH/AJ

Это равенство несообразно, ибо первое отношение меньше, а второе больше единицы, следовательно, и допущение (2) тоже не имеет места, откуда видно, что справедливо только равенство AOB/AOF = AB/AF (ЧТД).

Зная, что отношение углов равно отношению дуг, описанных равными радиусами, мы в пропорции (черт. 111)

AOB/COD = AB/CD

можем принять за единицу любую дугу. В этом случае должны принять за единицу и соответствующий ей угол.

Принимая дугу CD, а следовательно, и угол COD за 1, имеем равенство

AOB/1 = AB/1

или отношение угла к своей единице равно отношению дуги к своей соответствующей единице, откуда

∠AOB = ◡AB.

Это равенство означает, что

числовая величина угла равна числовой величине дуги, или что угол измеряется дугой, описанной из его вершины, как из центра.

Доказательство теоремы

Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.

Смотри, вот так:

Давай наберёмся мужества и докажем эту теорему.

Если ты читал уже тему «Биссектриса» разбирался в том, почему же три биссектрисы пересекаются в одной точке, то тебе будет легче, но и если не читал – не переживай: сейчас во всём разберёмся.

Доказательство будем проводить, используя понятие геометрического места точек (ГМТ).

Геометрическое место точек, обладающих свойством «\( \displaystyle X\)» – такое множество точек, что все они обладают свойством «\( \displaystyle X\)» и никакие другие точки этим свойством не обладают.

Ну вот, например, является ли множество мячей – «геометрическим местом» круглых предметов? Нет, конечно, потому что бывают круглые …арбузы.

А является ли множество людей, «геометрическим местом», умеющих говорить? Тоже нет, потому что есть младенцы, которые говорить не умеют.

В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:

Тут множество – это серединный перпендикуляр, а свойство «\( \displaystyle X\)» – это «быть равноудаленной (точкой) от концов отрезка».

Проверим? Итак, нужно удостовериться в двух вещах:

• Всякая точка на серединном перпендикуляре находится на одинаковом расстоянии от концов отрезка
• Всякая точка, которая равноудалена от концов отрезка – находится на серединном перпендикуляре к ему

Приступим:

Проверим 1. Пусть точка \( \displaystyle M\) лежит на серединном перпендикуляре к отрезку \( \displaystyle AB\).

Соединим \( \displaystyle M\) с \( \displaystyle A\) и с \( \displaystyle B\).Тогда линия \( \displaystyle MK\) является медианой и высотой в \( \displaystyle \Delta AMB\).

Значит, \( \displaystyle \Delta AMB\) – равнобедренный, \( \displaystyle MA=MB\) – убедились, что любая точка \( \displaystyle M\), лежащая на серединном перпендикуляре, одинаково удалена от точек \( \displaystyle A\) и \( \displaystyle B\).

Теперь 2. Почти точно так же, но в другую сторону. Пусть точка \( \displaystyle M\) равноудалена от точек \( \displaystyle A\) и \( \displaystyle B\), то есть \( \displaystyle MA=MB\).

Возьмём \( \displaystyle K\) – середину \( \displaystyle AB\) и соединим \( \displaystyle M\) и \( \displaystyle K\). Получилась медиана \( \displaystyle MK\). Но \( \displaystyle \Delta AMB\) – равнобедренный по условию \( \displaystyle (MA=MB)\Rightarrow MK\) не только медиана, но и высота, то есть – серединный перпендикуляр. Значит, точка \( \displaystyle M\) – точно лежит на серединном перпендикуляре.

Всё! Полностью проверили тот факт, что серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.

Это все хорошо, но не забыли ли мы об описанной окружности? Вовсе нет, мы как раз подготовили себе «плацдарм для нападения».

Рассмотрим треугольник \( \displaystyle ABC\). Проведём два серединных перпендикуляра \( \displaystyle {{a}_{1}}\) и \( \displaystyle {{a}_{2}}\), скажем, к отрезкам \( \displaystyle AB\) и \( \displaystyle BC\). Они пересекутся в какой-то точке, которую мы назовем \( \displaystyle O\).

А теперь, внимание!

Точка \( \displaystyle O\) лежит на серединном перпендикуляре \( \displaystyle {{a}_{1}}\Rightarrow OA=OB\);точка \( \displaystyle O\) лежит на серединном перпендикуляре \( \displaystyle {{a}_{2}}\Rightarrow OB=OC\).И значит, \( \displaystyle OA=OB=OC\) и \( \displaystyle OA=OC\).

Построение правильного четырехугольника вписанного в окружность

Вариант 1

Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.

Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.

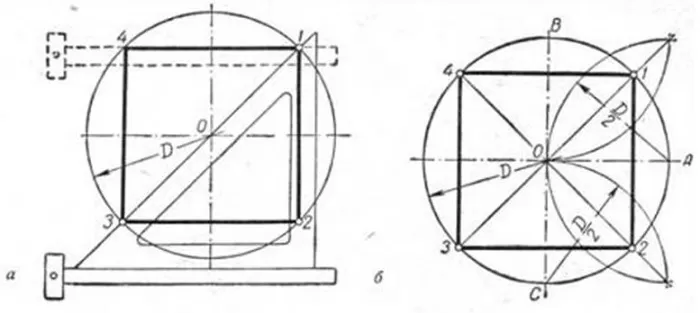
Вариант 2

Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.

После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.

Задача выполнена двумя способами.

Построение перпендикулярных прямых

Пример 1

Точка O находится на прямой a.

Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.

1. Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.
2. Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.

Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.

Доказательство, что прямая OC лежит перпендикулярно a.

Намечаются два отрезка — AC и CB. Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.

Пример 2

Точка O находится вне прямой а.

Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.

Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O1 — место их соприкосновения.

Рисуем линию, соединяющая т. O и т. O1.

Доказательство выглядит следующим образом.

Две прямые ОО1 и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO1A. Из данного вывода следует, что угол OAC = O1AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).

Исходя из этого, выводим, что угол OCA = O1CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.

Свойства окружности

1. Прямая может не иметь с окружностью общих точек; иметь с окружностью
   одну общую точку (); иметь с ней
   две общие точки (секущая).
2. Через три точки, не лежащие на одной прямой, можно провести окружность,
   и притом только одну.
3. Точка касания двух окружностей лежит на линии, соединяющей их центры.

Теорема о касательной и секущей

Если из точки, лежащей вне окружности, проведены
и , то квадрат длины касательной равен произведению
секущей на ее внешнюю часть: MC2 = MA•MB.

Теорема о секущих

Если из точки, лежащей вне окружности, проведены две ,
то произведение одной секущей на её внешнюю часть равно произведению другой
секущей на её внешнюю часть. MA•MB = MC•MD.

Шаг

Метод 1 из 3: рисование пересекающихся линий

1. Нарисовать круг.

   Компас — это устройство, специально разработанное для рисования и измерения кругов. Купите их в школе или магазине канцелярских товаров.

   Используйте компас или обведите круглые объекты. Размер круга не важен. Если вы хотите найти центр существующего круга, вам не нужно рисовать новый круг.

2. Между двумя точками протяните тетиву.

   При рисовании линий используйте карандаш. Таким образом, уже нарисованные отметки можно стереть после нахождения центра круга. Слегка нарисуйте его, чтобы его было легко стереть.

   Хорда — это прямая линия, соединяющая любые две точки на стороне круга. Назовите эту тетиву AB.

3. Нарисуйте вторую тетиву. Эта линия должна быть параллельна первой струне и иметь такую ​​же длину. Назовите эту тетиву CD.

4. Нарисуйте линию, соединяющую A и C. Этот третий аккорд (AC) будет проходить через центр круга, но вам нужно будет провести еще одну линию, чтобы найти точный центр круга.

5. Соедините точки B и D. Проведите последнюю линию хорды (BD) через круг между точками B и D. Эта новая линия прорежет третий проведенный аккорд.

6. Найдите центральную точку. Если вы проведете линию прямо и точно, центр круга будет там, где пересекаются линии AC и BD. Отметьте центральную точку ручкой или карандашом. Если вы хотите отметить только центральную точку, сотрите четыре нарисованные линии.

Метод 2 из 3: Использование пересекающихся кругов

1. Проведите линию, соединяющую две точки. С помощью линейки или прямого предмета проведите прямую линию внутри круга от одной стороны до другой. Можно использовать любую точку. Отметьте эти две точки буквами A и B.

2. С помощью циркуля нарисуйте два пересекающихся круга.

   Этот круг нарисуйте карандашом, а не ручкой. Процесс будет проще, если вы сможете удалить эти круги позже.

   Два круга должны быть одинакового размера. Используйте A как центр первого круга, а B как центр другого круга. Расположите два круга так, чтобы они пересекались, как диаграмма Венна.

3. Проведите вертикальную линию через два пересечения двух кругов. На «диаграмме Венна» есть точка вверху и точка внизу, образованная пересекающимися кругами. С помощью линейки проведите линию, идущую прямо от этих двух точек. Затем отметьте две точки (C и D) в точке пересечения с начальной окружностью. Эта линия отмечает диаметр исходного круга.

4. Удалите оба пересекающихся круга. Очистите бумагу перед выполнением следующего процесса. Теперь у нас есть круг с двумя перпендикулярными линиями. Не удаляйте точки A и B из этого круга! Мы собираемся нарисовать два новых круга.

5. Нарисуйте два новых круга. С помощью циркуля нарисуйте два круга равной величины: один с точкой C в качестве центра, другой с центром в точке D. Эти два круга также должны пересекаться, как на диаграмме Венна. Помните: C и D — это точки на вертикальной линии, пересекающей главный круг.

6. Проведите линию через пересечение этих двух новых кругов. Горизонтальная прямая линия пересечет область этих двух новых кругов. Эта линия является вторым диаметром исходной окружности и будет точно перпендикулярна первому диаметру.

7. Найдите центральную точку. Пересечение двух центральных линий — это положение центра круга! Отметьте эту центральную точку как ориентир. Если вы хотите очистить бумагу, просто сотрите все существующие линии диаметра и лишние круги.

Метод 3 из 3: использование прямых объектов на линейке треугольников

1. Нарисуйте две прямые касательные к сторонам круга. Эту линию можно провести с любого места. Однако этот процесс будет проще, если вы нарисуете две линии, которые приблизительно соответствуют квадратному или квадратному изображению.

2. Нарисуйте параллельные линии с первыми двумя линиями на противоположной стороне круга. Это дает нам четыре касательных к окружности, образующей параллелограмм или более или менее квадрат.

3. Нарисуйте диагонали параллелограмма. Пересечение диагоналей этого параллелограмма и есть центр окружности.

4. Проверьте точность этого центра с помощью компаса. Полученная вами центральная точка будет правильной, если вы не пропустите при рисовании линии или диагонали. Если хотите, можете удалить параллелограммы и диагональные линии.

Тройки и двойки

Когда старшая дочка пошла в первый класс, она была великолепно подготовлена, и я, разумеется, ждала от нее пятерок. Успехи ее сестры в детском саду тоже давали повод надеяться на отличную учебу в школе. Но очень скоро стало видно, что ни та, ни другая не блещут высшими баллами, а в 4-5-ом классе среди четвертных отметок местами забрезжили даже тройки. Мне нелегко было примириться с действительностью, и признать, что мои дети, похоже, «середнячки». Я никогда не ругала детей за двойки или тройки, но конечно, всегда ждала (и жду) от них большего. Однажды старшая дочка сказала: «Мама, когда я получаю двойку, ты расстраиваешься, и это хуже, чем если бы ты меня ругала». Сколько бы мы, родители, ни хвалились неординарным подходом, сколько бы ни выставляли напоказ равнодушное отношение к оценкам, мол, «оценки – это не главное», но, к сожалению, в большинстве случаев они все-таки показывают уровень знаний ученика, и его способность эти знания проявить в достаточно жесткой, стрессовой ситуации. А ведь в жизни таких ситуаций будет все больше и больше: ЕГЭ, сессия, запарка на работе – все это давит на психику не меньше, чем ответ у доски или итоговая контрольная.

Часто приходится слышать: «Он вообще-то умный и сообразительный ученик, все ошибки – от невнимания»

Дорогие родители, но ведь внимание – это не рубильник, который забыли повернуть при выполнении данного конкретного задания, но который непременно будет включен в следующий раз. Если от невнимания ребенок «хватает» тройки, значит, каким бы сообразительным он ни был, он, увы, не отличник, а троечник, и это реально тот уровень знаний, который он в состоянии продемонстрировать

Не надо себя обманывать. «Он может учиться лучше». Может, но не хочет. Или все-таки не может?

Расстояние между центрами окружностей

1. Если две окружности пересекаются в двух точках, расстояние центров меньше суммы и больше разности радиусов.

Действительно, с одной стороны (черт. 104)

OO’ < AO + AO’

с другой

AO + OO’ > AO’

следовательно,

OO’ > AO’ — AO

2. Если две окружности касаются, расстояние центров равно сумме радиусов, если соприкосновение внешнее, и разности радиусов, если соприкосновение внутреннее.

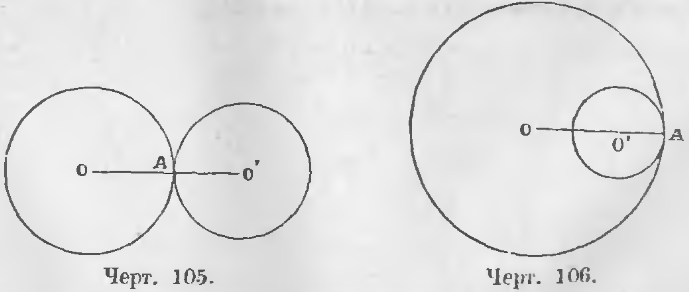
Из чертежа 105 видно, что

OO’ = AO + AO’

а из чертежа 106

OO’ = AO — AO’.

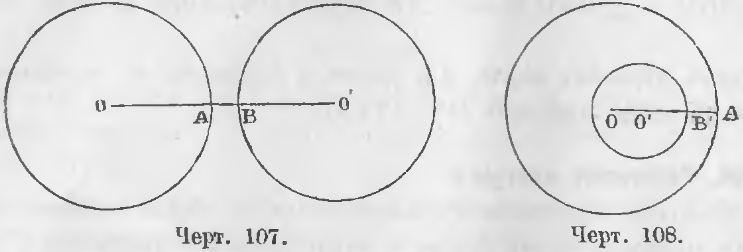
3. Если одна окружность лежит вне другой, расстояние центров больше суммы радиусов.

Из чертежа 107 видно, что

OO’ > AO + BO’

4. Если окружность лежит одна внутри другой, расстояние центров меньше разности радиусов.

Действительно, из чертежа 108 видно, что

OO’ < AO — BO’.

Почему возникают ошибки при измерениях

Наиболее распространенные ошибки, снижающие точность результатов измерений исправным инструментом:

• Чрезмерное давление на рамку вызывает перекос относительно штанги. Такой же эффект получается, если при измерении нижними губками сводить штангенциркуль за верхние.
• Установка губок на галтели, фаски и скругления.
• Перекосы при позиционировании.
• Нарушение калибровки инструмента.

Первые три ошибки чаще всего возникают от недостатка опыта, и уходят с практикой. Последнюю нужно предотвратить на этапе подготовки к измерениям. Проще всего выставить «0» на электронном штангенциркуле: для этого там предусмотрена кнопка (на рис. 6 кнопка «ZERO»). Часовой индикатор обнуляется вращением винта, расположенного в его нижней части. Чтобы откалибровать нониус, отпускают винты крепления к рамке, передвигают его в нужное положение и снова фиксируют.

Деформации элементов штангенциркуля и износ мерительных поверхностей делают инструмент непригодным к использованию. Для снижения количества брака на производстве штангенциркули проходят периодическую поверку в метрологических службах. Для проверки точности инструмента и приобретения навыков в бытовых условиях можно измерять детали, размеры которых заранее известны: например, хвостовики сверл или кольца подшипников.

Правило встречается в следующих упражнениях:

7 класс

Задание 18,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 180,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 631,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 698,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 5,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 713,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 895,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 7,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 10,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1131,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 6. Описанная окружность. Многоугольники

Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства. 

Около каких фигур можно, а вокруг каких нельзя описать окружность. 

Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью. 

Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.

ЕГЭ 6. Вписанная окружность

В этом видео мы узнаем, что такое вписанная окружность, где находится её центр, и другие свойства.

В какие фигуры можно, а в какие нельзя вписать окружность. Научимся решать задачи на вписанную окружность.

Понятие доли

Вы когда-нибудь заглядывали в тетради к старшеклассникам? Смотрите, какой у меня пример. 

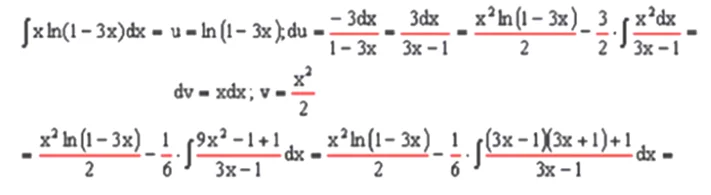
Видите сложение, вычитание, умножение? Знаки этих действий известны: плюс, минус, точка. Деление же в примере обозначено горизонтальной чертой.На рисунке она выделена красным цветом. Я расскажу, когда в математике используют черту.

Мы умеем делить несколько предметов, но часто деление нужно, чтобы раздробить одно число на равные части — доли от целой величины.

Один разделить на два — это одна вторая. Что же это такое?

В жизни вы часто так делали. Например, один апельсин делили с другом: брали нож и разрезали его пополам.

Каждый из вас получал половину или одну долю.

На лесной полянке собралось девять друзей, апельсин делили на всех. Рассмотрите рисунок. Как называется каждая часть фрукта? 

Совершенно верно, это долька. Апельсин поделили на 9 одинаковых долек.Каждая 1 долька апельсина — это одна из девяти равных долей целого фрукта.

Вы теперь поняли, ребята, что в жизни человеку приходится не только пересчитывать предметы, но и делить (дробить) целое на части, вот так появилось в математике понятие доли и дроби.

Знак доли (дроби) обозначают дробной горизонтальной или наклонной чертой. Например, так — 1/9 (одна девятая). Запись придумали арабы в 16 веке.

Доли называют по количеству частей раздробленного одного предмета:

• Разделите, например, яблоко на две равные части, у вас получится название доли «половина» или 1/2 (одна вторая)
• Разрежьте яблоко на три части. Один кусок — это «треть» — 1/3 (одна третья)
• Разломите на четыре доли — «четверть» — 1/4 (одна четвертая)

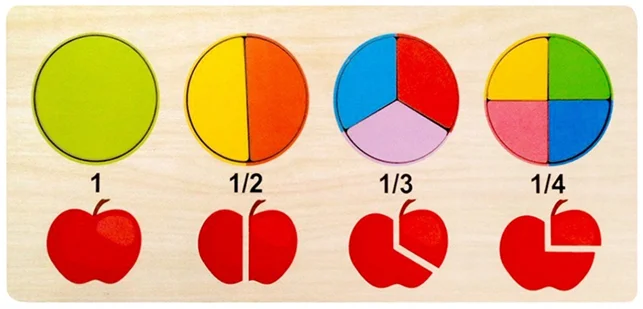
Знание о долях помогает решить задачи.

Запомните правило по математике нахождения доли.Чтобы найти долю от числа надо число разделить на эту долю. В дроби число, на которое делят, записано под чертой и называется знаменателем. То число, которое надо разделить, пишут над чертой. Это числитель.

Задание 1

Найдите пятую долю от числа 25. Это значит, что надо выполнить действие деления.

Привычный пример 25 : 5 можно записать вот таким образом:

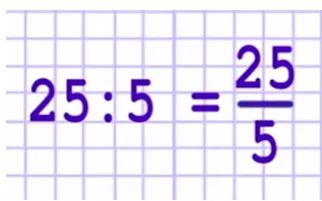
Или так — 25/5. 25 – это числитель, а 5 — знаменатель.

25: 5 = 5

Ответ: одна пятая доля от числа 25 равна пяти.

Задание 2

Чему равна 1/4 доля от полоски длинной 16 см?

Полоску согните пополам, ещё раз пополам. Разверните. На сколько долей линией сгиба разделили полоску? Правильно, на 4.

Закрасьте одну такую долю.

Какую долю вы закрасили? (одну четвёртую)

16 : 4 = 4(см)

Ответ: длина одной четвертой доли полоски составляет 4 см.

Задание 3

Решите задачи на понятие доли. Рассмотрите рисунки. Какая доля каждой фигуры закрашена серым цветом?

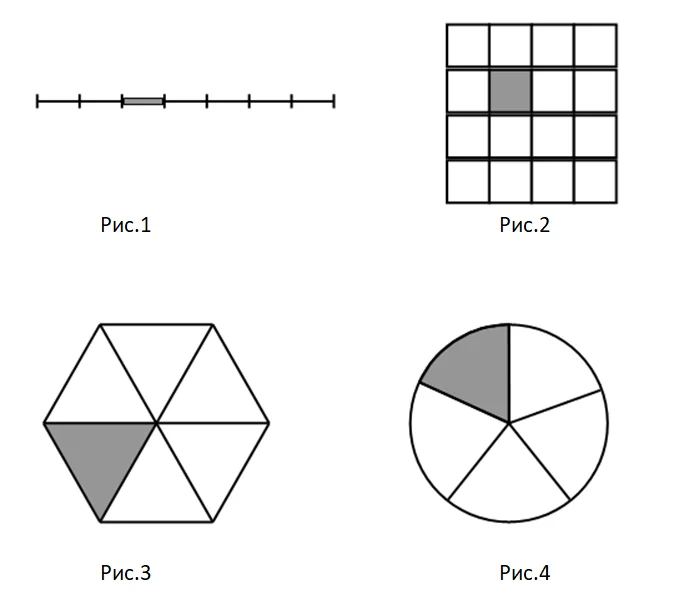
Рассуждаем так.

На рисунке 1 отрезок разделили на 7 частей.Значит, закрашена одна седьмая (1/7) доля фигуры.

Проверьте:

На следующих рисунках заштрихована 1/16 доля квадрата, 1/6 доля шестиугольника, 1/5 доля круга.

Чтобы разобрать понятие массовой доли, представьте себе килограмм яблок (1000 г), который мама купила своим трем детям.

Из этого килограмма самому младшему ребенку досталась половина всех яблок (несправедливо, конечно!). Старшему — лишь 200 г, а среднему — 300 г. 

Значит, массовая доля яблок у младшего ребенка составит половину, или одну вторую (1/2) массовую долю.

У старшего ребенка будет:

1000 : 200 = 5 — одна пятая (1/5) массовая доля

Далее рассуждаем так:

Младшему ребенку дали половину яблок.

1000 : 2 = 500(г)

Яблоки разделили между детьми по 500г, 200г и 300г. Вы знаете, что 500 — это 5 сотен, 200 — 2 сотни, 300 — 3 сотни.

На сколько сотен разделили все яблоки?

5 сотен + 2 сотни + 3 сотни = 10 сотен.

Сколько граммов будет в одной десятой доле?

1000 : 10 = 100 (г) в одной десятой доле

У среднего ребенка 300 г. Во сколько раз больше, чем 100 г?

300 : 100 = 3

В три раза. Значит, у среднего ребенка будет не одна, а три десятых массовых долей 3/10.

Ребята, вы молодцы. Верное решение.

Построение окружности

Для того, чтобы построить окружность используют специальный прибор, который называется циркулем (Рис.6). Циркуль состоит из двух частей, соединённых шарниром. Обычно на конце одной из них располагается игла, на конце другой — пишущий предмет, например грифель карандаша.

Выполнение построения:

• отмечаем точку, которая будет центром окружности;
• делаем нужный раствор циркуля (расстояние между иглой и грифелем карандаша), т.е. определяем радиус окружности, которую нам нужно построить (Рис.7);

• ставим иглу циркуля в точку, которая определяет центр окружности;
• проводим окружность данного радиуса (Рис.8).

Для того, чтобы построить окружность на местности используют веревку. Сначала отмечаем место, которое будет определять центр окружности, вбиваем в это место колышек, привязываем к нему один конец веревки и отходим, держа другой конец веревки на расстояние равное радиусу окружности, которую мы хотим получить, отмечаем линию окружности (Рис.9).

Часть плоскости, которая ограничена окружностью (выделена черным цветом), называется кругом (выделен голубым цветом) (Рис.10).

Похожие записи:

Руководства к лего technic Виды грядок из поддонов и как их сделать для дачи своими руками, ошибки Как убрать сколы на капоте без покраски Из чего состоит пластиковое окно? Как сделать копилку своими руками: фото и видео мастер-класс изготовления простых, красивых и оригинальных копилок Можно ли сажать тюльпаны весной: нюансы и правила посадки