Roll dice

Пример для 4d6k3

Рассмотрим, например sum(4d6k3):

Математическое ожидание: 12.2, т.е. усреднённое значение всех бросков близко к 12, но несмотря на это чаще всего выпадает 13 (распределение не симметричное)
среднеквадратичное отклонение: 2.8, т.е. значения с 12.2 по 12.2+2.8 (т.е. реально 13,14,15) выпадают с вероятностью примерно 34%. Однако это распределение отличается от Гауссового, и в реальности вероятность выпадения этих значений будет 13%+12%+10% =35%, что не сильно отличается от нормального распределения
В общем случае вероятность выпадения значений в определённом диапазоне можно посчитать просто суммируя вероятности каждого из этих значений. Например: вероятность выкинуть 9 или меньше: (0.08+0.31+0.77+1.6+2.9+4+7)% ≈ 17%

Графики плотности вероятностей для sum(2d6), sum(3d6), sum(3d6k3), 1d6! (со взрывами):

изменение кубической формы кости

Здесь есть несколько вариантов. Прежде всего, изменение кубической формы. Представьте, как может повлиять на бросок кости, если хотя бы одна из граней скошена немного под другим углом. А если игральная кость вовсе не куб? А ведь и такое провернуть не сложно. Буквально сточенная пара миллиметров изменяет куб на прямоугольный параллипипед, где более широкая грань имеет больший шанс на выпадение. Возможно и иное: одна из граней выпуклая, что фактически исключает ее из комбинации.

Такие шулерские кости, механически изменненные, широко использовались в игре крэпс, где комбинация «семь» или «одиннадцать» являются выгодными уже на первом поинте. Незаметная подмена костей казино на свои «нужные» кости позволяли шулерам выигрывать. Да что там говорить о шулерах! На заре становления игрорного бизнеса, сами игорные заведения нередко прибегали к шулерским приемам, подменяя игральные кости на такие, где как раз эти самые 7 и 11 не выпадали. Стикмэн очень ловко вводил и выводил такие неправильные кости в крэпсе, изменяя преимущество казино в его сторону.

Хочу Вам сказать, что и вогнутая грань, создавая эффект вакуума, также может повлиять на бросок, особенно, если бросок совершается на грубой поверхности.

Механическое изменение граней кубика, порой совсем незаметное для глаза, также может повлиять на результат игры. Стандартный скошенный угол грани — 45 градусов. Изменние скоса нескольких граней до шестидесяти изменяет бросок. Так же влияет на бросок и более острый, чем стандартный угол грани. Безусловно, в броске игральная кость будет тяготеть остановиться на более остром угле.

Вот такой набор найден мной на просторах Интернета в продаже. Предлагается изготовить игральные кости со смещением центра тяжести, причем Вы можете выбрать, какую же грань «убрать» из броска, т.е. утяжелить.

Трактовка результатов

В процессе определения своего будущего обычно интересуются следующим:

Определяются шансы на исполнение конкретного желания.
Выясняют, чего можно ожидать в будущем и на что нужно обратить особое внимание.

При бросании одного кубика результат определяется тем, сколько очков выпало на ней:

Если на верхней грани единица, то это говорит о счастливом и удачливом человеке. В этом случае тот путь, которого придерживается человек, является правильным и позволяет надеяться на успех в дальнейшем.
Если выпала двойка, нужно быть готовым к переменам. Такой результат говорит не только о дальнейших изменениях, но и о тех, которые только начались. Нужно внимательно присмотреться к своей ситуации и постараться определить правильное направление своего дальнейшего движения.
Значение, равное тройке, выгодно для тех, кто занимается своим проектом. Такой исход броска говорит об успешности начинания, но не исключает того, что предпринимателю за свой успех придётся заплатить сильным нервным перенапряжением.
Четвёрка благоприятна для творческих людей

Неважно, в какой области он действует, такой исход гадания говорит об успешном воплощении замыслов.
Если выпала пятёрка, это подчёркивает, что тот, кто производит гадание, склонен к излишнему авантюризму. В этой ситуации особенно важно продумывать свои шаги, иметь план дальнейших действий.
В последнем случае, при выпадении шестёрки, результат подчёркивает стабильность и надёжность положения

Человек, выбросивший кубики, уверен в себе. В этой ситуации важно не переоценить свои силы, демонстрируя излишнюю самоуверенность.

Если использовались два кубика

Если определение будущего производится с использованием двух кубиков, результат можно трактовать в зависимости от полученных результатов. Вот несколько примеров:

Если на игральных костях кубиках получились единицы, это говорит о счастье и об успехе. В этой ситуации не требуется предпринимать дополнительные усилия для улучшения ситуации в дальнейшем.
При варианте 1+2 для женщины это говорит о браке ради денег. Если говорят о мужчине, то такой исход указывает на развлечения, за которые заплачены деньги

Считается, что проводить больше времени дома поможет несколько улучшить свою ситуацию.
Когда выпало 1 и 3 — это свидетельствует о будущих серьёзных неприятностях.
Если было 1+4, движение, активность, получение новой информации — это то, что важно в ближайшее время.
Если выпали единица и пятёрка, то речь идёт о хлопотах, которые имеют тенденцию в конце концов окончиться благоприятно.

В зависимости от выпавших значений можно определить, чего стоит ожидать в дальнейшем и как действовать, чтобы повысить шансы на успех.

Покер на костях: разновидности

Существует несколько разновидностей покера на костях:

Игра в которой можно получить бонус за выпадение каре. Дополнительно к этому идет подсчет неиспользуемых бросков участником. Если он не участвовал в каком-либо из дальнейших этапов, к его сумме добавляется по три балла за каждый из неиспользуемых этапов. В такой игре на первом этапе необходимо выполнить обязательно сочетание.

Следующий вариант игры позволяет своим участникам получать 50 бонусных баллов за выпадение комбинации покер. При этом не учитывается какие номиналы выпали – 50 баллов это фиксированный бонус. Также в таком варианте игры не берутся в учет комбинации состоящие из четных или нечетных костей. Кроме этого, в этом варианте игрок может играть любой набор из таблицы.

Классическая игра. Каждый участник имеет право выполнить три броска. Ему необходимо сформировать несколько комбинаций из 5 костей. Однако существует одно ограничение. Игрок не может перекидывать кости, выпавшие на первом броске. В дальнейшем их можно использовать для формирования комбинаций. Далее начинается подсчет выигрышных комбинаций и баллов. После этого высчитывается ранг игроков. Он зависит от силы комбинаций и количества заработанных балов. Игроку с самым высоким рангом достаются все деньги. В классической игре учитываются все выпадающие комбинации костей.

Игральные кости онлайн — бросить кубик

Кости – одна из древнейших игр в мире, которая насчитывает тысячелетия. Их изначально делали из костей животных, а если верить мифам и легендам, еще и костей человека, отсюда и происходит их название и определенная мистическая аура. В кости играли в Древнем Египте, Риме, Индии, откуда они с развитием торговых и культурных связей проникли в Западный мир. Сегодня самым популярным вариантом игры в кости является крэпс – в него играют как дома, так и в казино, в том числе онлайн-казино. Всего же существует несколько десятков разновидностей этой игры.

Основной принцип игры простой и всем понятен – игроки бросают кости, сумма выпавших очков на костях подсчитывается. Сами по себе игральные кости используются в самых разных настольных играх, заставляя выполнять различные действия на карте. И, конечно, без них не обходится ни одно казино мира. Однако чтобы поиграть в кости можно использовать различные программы и приложения, такие как наш кубик онлайн.

Вы здесь

Главная › Инженеру-конструктору › 4. Полезные схемы для радиолюбителей › 3. Электронные игры.

3.1 Электронный кубик.

сб, 04/01/2006 — 21:19 — admin

3.1 Электронный кубик

Всем знакомы игры, в которых перед началом хода требуется бросать небольшой пластмассовый кубик, на шести гранях которого нанесено от одной до шести точек (очков). Бросая по очереди кубик, играющие суммируют очки: кто больше набрал, тот и выиграл.

Можно изготовить электронное устройство, заменяющее такой кубик. На передней панели устройства должны быть шесть светодиодов, кнопка и тумблер включения. Стоит нажать кнопку — и количество светящихся светодиодов покажет число набранных в очередном туре очков.

Принципиальная схема электронного кубика представлена на рис. 17,а. На трех логических элементах 2И-НЕ микросхемы DD1 собран генератор, а на шести D-триггерах (микросхемы DD2-DD4) -кольцевой счетчик.

Как работает генератор? Он представляет собой трехкаскадный усилитель, охваченный положительной обратной связью через конденсатор С1 и отрицательной — через резистор R1. При наличии таких связей в усилителе возникают автоколебания, частота которых определяется произведением R1C1. При этом контакты кнопки SB1 должны быть разомкнуты. Запомните эту схему — в дальнейшем она будет использоваться во многих устройствах.

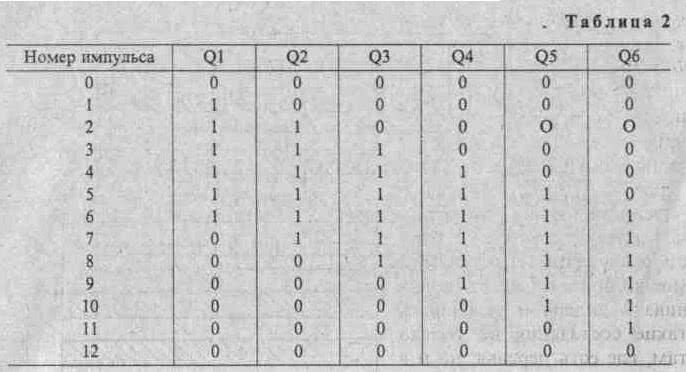
Рассмотрим работу счетчика. Как видно из схемы, все синхронизирующие входы D-триггеров соединены между собой, а вход D последующего триггера соединен с прямым выходом предыдущего D-триггера. Вход же D первого триггера (DD2.1) соединен с инверсным выходом последнего триггера (DD4.2). Работу цепи триггеров (ее еще называют кольцевым триггерным счетчиком) удобно проанализировать по таблице истинности (табл. 2). Выходы Q1-Q6 — это прямые выходы триггеров. Допустим, в исходный момент все триггеры находятся в нулевом состоянии. Тогда на входе D первого триггера — напряжение высокого уровня, поступающее с инверсного выхода шестого триггера. После поступления первого импульса триггер DD2.1 переключается в единичное состояние, и с его прямого выхода напряжение высокого уровня поступает на вход D триггера DD2.2. .Поэтому после поступление импульса № 2 второй триггер переключается в единичное состояние По мере поступления на входы С шести, импульсов все триггеры

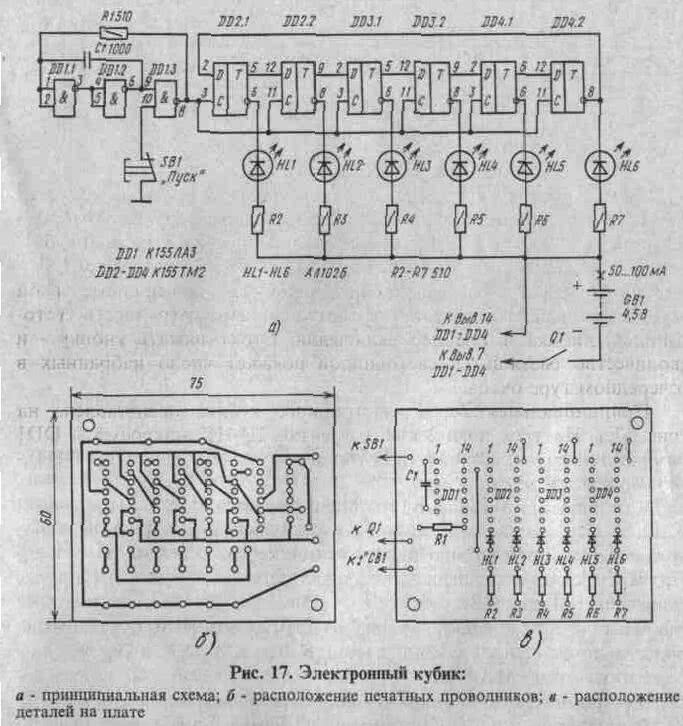
переключаются в единичное состояние. При этом светятся все светодиоды, подключенные к инверсным выходам триггеров. На вход D первого триггера теперь подано напряжение низкого уровня, и при подаче последующих шести импульсов триггеры последовательно переключаются в нулевое состояние. Из табл. 2 видно, что период работы кольцевого счетчика равен 12 тактам.

При нажатии кнопки SB1 «Пуск» импульсы частотой 1…2 МГц с генератора поступают на вход кольцевого счетчика. Последний за время удержания кнопки (1…2 с) многократно переполняется, поэтому после отпускания кнопки состояния триггеров DD2.1 -DD4.2, отображаемые горящими светодиодами HL1-HL6, практически случайны. Сколько светодиодов зажглось, столько очков и записывают в актив игроку.

Питаются микросхемы от батареи GB1, потребляя ток 50…100 мА.

Все элементы устройства, кроме SB1, Q1 и GB1, расположены на печатной плате (рис. 17, б,в). Выключатель питания Q1 (он может быть типов П2Т, МТ1, П2К) и кнопка SB1 (она может быть типов КМ1, МП1 или любого другого типа) расположены на верхней крышке. Здесь же просверлены отверстия для светодиодов HL1-HL6. Плата с деталями крепится с помощью винтов с ограничивающими втулками. Батарея GB1 может быть типа 3336 «Рубин»; светодиоды HL1-HL6 — типов АЛ102, АЛ307 АЛ310 с любыми буквенными индексами; конденсатор С1 — типов КЛС, КМ-5, К10-7в, К10-23;

резисторы — типа МЛТ-0,25.

Электронный кубик в налаживании не нуждается.

Начинающие радиолюбители могут «увидеть», как переключаются триггеры при поступлении импульсов генератора. Для этого параллельно конденсатору С1 необходимо подключить оксидный конденсатор емкостью 200…500 мкФ на напряжение 6…10 В отрицательной обкладкой к выводам 1, 2 логического элемента DD1.1. При этом частота генератора уменьшится до 0,5…2 Гц, и по зажиганию соответствующих светодиодов можно проследить последовательность переключения триггеров. Разумеется, кнопка SB1 должна быть постоянно нажата.

Как, кидая кубик, получить любую вероятность?

В школе я увлекался настольными играми, в основном варгеймами. Придумывал правила, изготавливал поля, юниты и проводил с друзьями увлекательные баталии. Однако вскоре для моделирования различных игровых ситуаций перестало хватать стандартного игрового кубика, с помощью которого можно получать вероятности, кратные одной шестой. Поиск решения породил пару интересных математических задач, связанных с теорией вероятности.

Итак, допустим, имея игровой кубик, нам нужно получить событие, вероятность которого равна 1/5. Для этого рассмотрим такой процесс: кубик бросается до тех пор, пока на нём не выпадет число, не равное шести. Очевидно, что в конечном итоге вероятности получить одно из чисел от 1 до 5 будут равны 1/5. Найдём, какое в среднем количество бросков потребуется сделать, чтобы серия шестёрок завершилась другим числом (иными словами, математическое ожидание данное величины).

С вероятностью

Её несложно будет вычислить, представив в следующем виде:

В итоге математическое ожидание количества бросков для получения результата равно 1,2.

Рассмотрим теперь, как получать события с вероятностями, меньшими 1/6. К примеру, как сделать механический генератор случайных чисел от 1 до 36. Для этого можно обратиться к помощи систем счисления. Тридцать шесть чисел от 0 до 35, записанные в шестеричной системе счисления будут двузначными, от 00 до 55. Таким образом, если взять два кубика, таких, чтобы по виду можно было определить, какой из них первый, а какой второй, и нанести им на грани цифры от 0 до 5, каждый бросок будет нам давать случайное число от 0 до 35, записанное в шестеричной системе. Чтобы исключить необходимость оперирования недесятичной системой и получать числа из диапазона 1..36, нанесём на один кубик числа 1, 2, 3, 4, 5, 6, а на другой – 0, 6, 12, 18, 24, 30.

Если же нам необходимы случайные числа от 1 до 18, то на первый кубик наносятся числа от 1 до 6, а на второй: 0, 0, 6, 6, 12, 12.

Объединив оба подхода, можно с помощью трёх кубиков получать события с вероятностями, кратными 1/100. Для этого возьмём 3 кубика, два, такие, как в системе, дающей числа от 1 до 36, а на грани третьего нанесём числа 0, 0, 36, 36, 72, 72. С её помощью будем получать числа от 1 до 108. Если теперь при выпадении значений от 101 до 108 бросать кубики снова, и останавливаться только в случае получения числа от 1 до 100, мы сможем замоделировать любую вероятность, кратную целому числу процентов. Даже для самых сложных правил настольных игр этого должно хватить.

По мотивам этой темы можно составить задачу. Имеется арифметическая прогрессия a 1 , a 2 , a 3 , … с разностью d, и геометрическая прогрессия b 1 , b 2 , b 3 , … со знаменателем -1 1 b 1 +a 2 b 2 +a 3 b 3 +…. Разобравшись с тем, как мы находили математическое ожидание количества бросков, её решить будет несложно.

Поздравляю Вас с наступающим Новы Годом и желаю, чтобы все возможные расклады были для Вас удачными!

Источник

Шаг третий. Собираем счётчик нажатий

Подключу кнопку одной ножкой к общему минусу, второй — к контакту 13 на Ардуино.

Я выбрал 13 контакт не случайно, на борту платы рядом с ним расположен оранжевый светодиод. Он будет гореть, когда кнопка отпущена и гаснуть, когда нажата. Почему, так происходит — расскажу в следующем проекте. Пока же воспользуюсь этим, чтобы проверить схему.

Изменю предыдущую программу так, чтобы значение счётчика менялось только при нажатии на кнопку.

Получился простой счётчик, похожими устройствами (их иногда называют кликеры) часто пользуются стюардессы, чтобы пересчитать пассажиров на борту самолёта.

Dungeons & Dragons

Большинство проверок сводится к «выбросить на 1d20 больше чем DC-skill» или к аналогичным. Для данной простой проверки даже графики-то не нужны, всё можно посчитать в уме. Вероятность выкинуть 10 или больше: 1/20*11 = 55%. Вероятность выкинуть 15 или больше: 6/20 = 30%

немного сложнее с новой системой Advantage/Disadvantage, когда бросается 2d20, и берется лучшее/худшее значение: min(2d20) и max(2d20). Вот графики для них:

При наличии advantage вероятность выбросить 20 — почти 10%! Аналогичная вероятность выкинуть 1 при disadvantage. Плотности вероятности обоих вариантов являются зеркальными отображениями друг-друга, поэтому свойства одной «зеркально» являются свойствами другой.
Математическое ожидание смещается на 3.3 вправо или влево. Однако распределение не Гауссово, и даже не похоже на изначальное, так-что это не эквивалентно бонусу/штрафу 3.3
при advantage вероятность получить 9 или меньше 20%, в то время как на обычном 1d20 —45%

Броски 2dN с выбором лучшего/худшего хороши для процессов вида «чем больше, тем вероятнее» или «чем меньше тем вероятнее», например при случайном выборе «силы» для воина, или при выборе количества трезвенников в баре, количество проституток в церкви, количество честных людей в правительстве, средняя школьная оценка мелкого воришки, вероятность что кошка приземлится на ноги. Так же эти броски хороши для описания процессов которые следуют закону Мерфи, например вероятность что бутерброд упадёт маслом вниз.

Хоббиты

Везучие хоббиты могут перекидывать кубик, если на нём выпало значение 1. Если вам интересно как это влияет на вероятности выбросить то или иное значение, то можете изучить следующие графики

Тут всё просто: вероятность получить 1 — 1/5

При наличии преимущества, вероятность получить 1 у халфлинга меньше одной тысячной процента, а остальное видно на графике

Покер на костях

Техасский холдем и покер на костях имеют отличия

Во-первых, если в классическом покере игроки получают карманные карты и строят сильнейшие комбинации, то, чтобы играть в покер на костях, участники должны бросать кости и подсчитывать очки.

Во-вторых, в классическом покере игроки начинают ходить от баттона, а в покере на костях игру начинает участник, который смог выбросить больше всех очков.

В-третьих, существует ограничение по количеству игроков. Если в классическом покере за столом может находится до 10 человек, то к этой вариации количество участников может быть неограниченным.

использованная литература

Gygax, Гэри; Арнесон, Дэйв (1974). Dungeons & Dragons, Книга I: Люди и Магия . Женевское озеро, Висконсин: TSR. п. 33.
Gygax, Гэри; Арнесон, Дэйв (1974). Dungeons & Dragons, Книга II: Монстры и сокровища . Женевское озеро, Висконсин: TSR. п. 3.
Там же.
Там же.
Gygax, Гэри (1978). Продвинутые подземелья и драконы . Женевское озеро, Висконсин: TSR.
Гэри Гайгакс, Advanced Dungeons & Dragons Dungeon Masters Guide, стр. 10: «при условии использования стандартного d20, который пронумерован дважды от 0 до 9».

Зима, Стив (2007-03-02). «Краткая история игры в кости» . Волшебники побережья . Проверено 6 марта 2007 .

Приложение «Fun2Create» создано известной художницей Мэй Ю.

Приложение (Андроид, iOS) предоставляет широкие возможности по конструкции нужного персонажа, позволяя сконструировать его уникальный визуальный стиль. После создания персонажа вы можете поделиться им на Фейсбук или сохранить на своё мобильное устройство, использовав его в дальнейшем в качестве аватара. Программа полностью бесплатна, и никаких покупок от вас не потребуется.

ePIC Character Generator на Android

«ePic Character Generator» (Андроид) – отличный инструмент для тех, кто хочет создать реалистичные аватары персонажей. Вы можете выбрать элементы отображения на вашем персонаже, сохранить как изображение на предустановленном или прозрачном фоне, и использовать его для всего, чего захотите. Создание персонажа в приложении проходит очень просто и сводится к нажатию нескольких кнопок.

Данная программа часто используется ролевыми игроками для иллюстрации игровых и неигровых персонажей. Персонажи могут быть сохранены и загружены с использованием специального формата файла. Созданные персонажи разрешается использовать в коммерческих продуктах.

FaceQ на IOS

FaceQ (iOS) — очень увлекательная и мощная программа для создания аватаров. Даже если вы не умеете рисовать, вы все равно можете легко создать свой собственный мультяшный аватар, комбинируя различные части лица.

https://youtube.com/watch?v=_QxDevr4-l0

Ингредиенты (Необязательно) Случайный выбор изВ игреСделано вами

Ингредиент 1: НетАКРОКАНТОПСАКРОКАНТОЗАВРАЛАНКИЛОЗАВРАЛАНКААЛЬБЕРТОЗАВРАЛЛОРАПТОРАЛЛОЗАВРАЛЛОЗАВР МОД. 2АЛЛОСИНОЗАВРАМАРГАЗАВРАМАРГОЦЕФАЛАМФИЦИОНЭНДРЮСАРХЭНДРЮТЕРИУМЭНДРЮТОДОНАНКИЛОКОДОНАНКИЛОЗАВРАНКИЛОЗАВР МОД. 2АНКИНТРОЗАВРАНТАРКТОПЕЛТААПАТОЗАВРАКВИЛАМИМУСАРАМБУРГИАНААРХЕОПТЕРИКСАРХЕОТЕРИЙАРКТОПСАРДОНТОЗАВРАРГЕНТАВИСАРГЕНТЕРИКСАРГЕНТИНОЗАВРБАЙАДОЗАВРБАРИОНИКСБАРИОНИКС МОД. 2БЛЮБРАХИОЗАВРБРОНТОЛАСМУСБРОНТОТЕРИЙБАМПИКАРБОНЕМИСКАРБОТОЦЕРАТОПСКАРНОТАВРЧАРЛИКОЭЛХААСТЦЕЛЮРОЗАВРАВУСКОМПСОКАУЛУСКОМПСОГНАТКОМПСОГНАТ МОД. 2КОНКАВЕНАТОРДАКОТАНОПСДАКОТАРАПТОРДАРВИГОПТЕРИКСДАРВИНОПТЕРДЕЙНОХЕЙРДЕЙНОНИХДЕЙНОТЕРИУМДЕЛЬТАДИЛОФОБОАДИЛОФОЗАВРДИЛОФОЗАВР МОД. 2ДИЛОРАНОЗАВРДИМЕТРОДОНДИМЕТРОДОН МОД. 2ДИМОДАКТИЛДИМОРФОДОНДИПЛОКАУЛУСДИПЛОКАУЛУС МОД. 2ДИПЛОДОКДИПЛОТАТОРДИПЛОВЕНТОРДОДОДОДОЦЕВИЯДЕДИКУРУСДРАКОЦЕРАТОПСДРАКОРЕКСДРАКОРЕКС МОД. 2ДЖУНГЕЯДЖУНГАРИПТЕРЭХОЭДАФОЦЕВИЯЭДАФОЗАВРЭДМОНТОГУАНОДОНТЭДМОНТОЗАВРЭЙНИАЗУХЭЙНИОЗАВРЭЛАСМОТЕРИЙЭНТЕЛОХОПСЭНТЕЛОДОНЭНТЕЛОМОНТЭРЕМОЦЕРОСЭРЕМОТЕРИЙЭРЛИКОГАММАЭРЛИКОЗАВРЭРЛИКОЗАВР МОД. 2ЭУКЛАДОЦЕРОСЭВОПЛОЦЕФАЛГАЛЛИМИМЖИРАФОТИТАНГЛИПТОЦЕРАСГЛИПТОДОНГОРГОНОПСГОРГОЗАВРГОРГОЗУХГРИЛЕНКЕНГРИПОЗУХОРЕЛ ХААСТАОРЕЛ ХААСТА МОД. 2ГАТЦЕГОПТЕРИКСИГУАНОДОНИНДОМИНУС РЕКСИНДОМИНУС РЕКС МОД. 2ИНОСТЕРИЙИНОСТРАНЦЕВИЯИРРИТАТОРИРРИТАТОР МОД. 2КАПРОЗУХКЕЛЕНКЕНКЕНТРОЗАВРКЕРАТОПОРКУСКУЛАБУРГИАНАКУЛАЗУХКУЛАЗУХ МОД. 2ЛИТРОНАКСМАЙАЗАВРМАЙЮНДАЗУХМАЙЮНГАЗАВРМАМОНТЕРИЙСУМЧАТЫЙ ЛЕВМЕГАЛОЦЕРОСМЕГАЛОГЕЯМЕГАЛОНИКСМЕГАЛОЗАВРМЕГАЛОТОПСМЕГИСТОЦУРУСМЕГИСТОТЕРИЙМИОЛАНИЯМИРАГЕЯМОНОЛОМЕТРОДОНМОНОЛОФАЗАВРМОНОЛОФАЗАВР МОД. 2МОНОМИММОСХОПСНАСУТОЦЕРАТОПСНОДОПАТОЗАВРНОДОЗАВРНУНДАЗУХОФИАКОДОНОРНИТОМИМУРАНОЗАВРОВИЛОФОЗАВРОВИРАПТОРПАХИЦЕФАЛОЗАВРПАРАМОЛОХПАРАЗАУРОЛОФПАРАЗАУЛОРОФ ЛЮКСФОРОЗАУРАФОРОРАКОСПОСТИМЕТРОДОНПОСТОЗУХПУАКАЙДЕЙПРОЦЕРАТОМИМПРОЦЕРАТОЗАВРПТЕРАНОДОНПТЕРАКЕТЦАЛЬПУРУОЛИТПУРУСЗАВРПУРУСЗАВР МОД. 2ПУРУСТАВРПИРОРАПТОРПИРРИТАТОРКЕТЦАЛЬКОАТЛЬРАДЖАКИЛОЗАВРРАДЖАЗАВРРИНХЕНИАРИНХИЦИОНСАРКОЗУХСКАФОГНАТСКОЛОЗАВРСКОРПИУС РЕКС МОД. 2СКУТОФИЦИОНСКУТОЗАВРСЕКОДОНТОЗАВРСИНОЦЕРАТОПССКУЛОЗАВРСМИЛОЦЕФАЛОЗАВРСМИЛОДОНСоноразаврСПИНОНИКССПИНОЗАВРСПИНОЗАВР МОД. 2СПИНОТАРАПТОРСТЕГОЦЕРАССТЕГОЦЕРАТОПССТЕГОЗАВРСТРУТИОМИМСТИГИМОЛОХСТИГИМОЛОХ МОД. 2ЗУХОМИМЗУХОТАТОРТАНИКОЛАГРЕЙТАРБОЗАВРТЕНОНТОЗАВРТИТАНОБОАТИТАНОБОА МОД. 2ТРИЦЕРАТОПСТРИЦЕРАТОПС МОД. 2ТРООДОНЦИНЬТАМОТЦИНЬТАОЗАВРТОДЗЯНГОЗАВРТУПАНДАКТИЛУСТИРАННОЛОФОЗАВРТИРАННОЗАВРТИРАННОЗАВР МОД. 2ЮТАРАПТОРЮТАЗИНОРАПТОРВЕЛОЦИРАПТОРВЕЛОЦИРАКОСШЕРСТИСТЫЙ МАМОНТШЕРСТИСТЫЙ НОСОРОГУЭРХОЗАВР

Суеверия[]

Из-за значимости бросков во многих системах и стилях игры, а также известного психологического эффекта, за счёт которого необычные броски в напряжённой и значимой ситуации запоминаются лучше, среди ролевиков ходят многочисленные байки относительно «разумного поведения» или «характера» кубиков (см, например, «Дайсы правду знают»), от чисто юмористических до вполне серьёзных. Нередко также игроки любят те или иные комплекты костей, считают их «удачливыми» или «неудачными», предпочитают делать броски в значимых ситуациях сами и так далее. Некоторые реальные основания под этим (например тот факт, что далеко не все дайсы являются хорошо сбалансированными и кости, особенно разнокомплектные и старые, могут отличаться по шансам выпадения какого-то числа на величину, заметную и не при долгом тестировании) оказываются многократно преувеличены и погребены под слоем шутливых или полушутливых толкований. В качестве примера можно привести шутку про Чёрные Мастерские Дайсы.

Мошеничество с игральными костями

В раскопанных погребениях на всех континентах попадаются игральные кости, выполненные специально для нечестной игры. Они имеют форму неправильного куба. В результате наиболее часто выпадает самая длинная грань. Неправильность формы достигается стачиванием одной грани. Еще куб можно трансформировать в параллелепипед. Эти неправильные кости получили прозвище «болванок». Он считаются атрибутом шулерской игры, и, как правило, принадлежат мошенникам.

Современную болванку внешне невозможно отличить от обычной кости, поскольку она имеет форму идеального куба. Но в болванке одна или несколько граней имеют дополнительный вес. Такие грани и выпадают чаше других.

Еще одна уловка заключается в дубляже граней – одних достаточно много, другие напрочь отсутствуют. В результате одни цифры будут выпадать слишком часто, а другие – почти никогда. Эти кости называют «вершками и донышками». Такие изделиями пользуются мошенники с большим опытом и довольно ловкими руками. Обычный игрок зачастую не замечет, что его партнер ведет нечестную игру.

Некоторые мошенники много тренируются с нормальными костями. В результате у них получается выкидывать требуемые комбинации. С этой целью кости бросаются специальным способом, позволяющим одному или двум изделиям вращаться в вертикальной плоскости и ложиться на требуемую грань.

Другие жулики выбирают мягкую поверхность в виде одеяла или пальто. По такой поверхности кость катится наподобие катушки. В итоги боковые грани почти не выпадают, что приводит к нежелательным для соперника комбинациям.

Шаг второй. Выводим цифры

Пока индикатор зажигает отдельные сегменты, но чтобы вывести цифры нужно научиться зажигать комбинации. По принципу это напоминает заполнение почтового индекса. Попробуем вывести цифру 1. Для этого нужно определить, какие сегменты зажигать. Посмотрим схему подключения более внимательно.

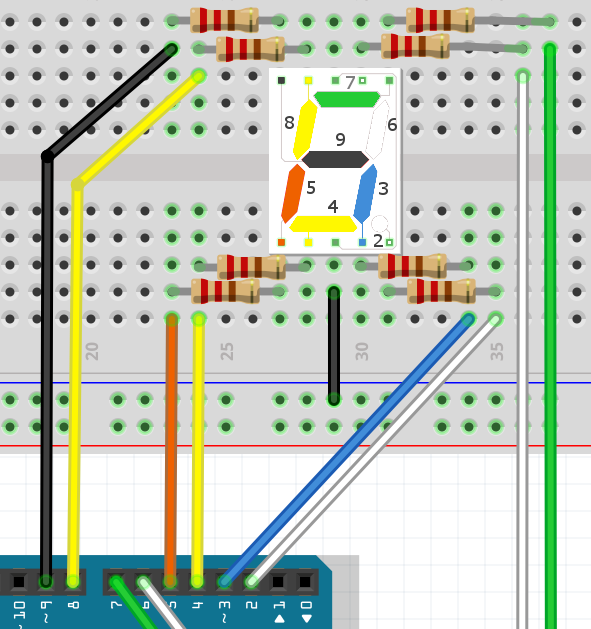
Чтобы вывести на экран цифру 1, нужно зажечь два правых сегмента. Они подключены белым и синим проводами к контактам 3 и 6. Изменю тестовую программу, чтобы она выводила на экран единицу.

Это уже что-то. Аналогично подберу сегменты, чтобы вывести остальные цифры. Соберу эту информацию в массив. Массив — это переменная, которая содержит сразу несколько значений. Каждое отдельное значение называется элементом массива. Такой элемент можно вывести, если знать его номер.

Мне нужен массив из 11 элементов: десять для цифр от 0 до 9 и один для точки.

Каждый элемент моего массива начинается со служебной комбинации символов 0b, которая означает, что элемент состоит из двоичных данных. А дальше идёт комбинация из восьми нулей или единиц. Они задают сегменты, которые будут гореть: 1 включит сегмент, 0 — выключит.

Запущу простую программу, которая будет последовательно выводить все элементы массива на экран.

Элементы готовы, остаётся добавить кнопку, которая будет управлять моим устройством.