Юный техник — для умелых рук 1986-12, страница 15
Секреты мастерства 3ВG3ДЧЯТЫв
МНОГОГРАННИКИ
Приглашаем вас на необычный урок геометрии, где вы научитесь построению звездчатых многогранников. В основе их лежат строгие математические закономерности.
Изготовив хотя бы одну такую звезду, вам, наверное, захочется «открыть» и другие. Своим разнообразием эти геометрические фигуры напоминают фантастические звезды, планеты, астероиды. Причем среди них, вероятно, есть и такие, которые еще никому не удавалось рассчитать и построить. Может, это Сделаете вы? Только начинать работу надо с азов.
Познакомившись с техникой изготовления простых звездчатых многогранников, вы сможете украсить рукотворными звездами актовый зал школы для новогоднего бала, свою комнату, елку. А почему бы не подарить такую звездочку ветерану, другу, не устроить выставку, где вы посоревнуетесь с друзьями в фантазии?
С глубокой древности математикам были известны пять выпуклых многогранников, которые называют Платоновыми телами. Это известные, наверное, каждому школьнику тетраэдр, гексаэдр, октаэдр, икосаэдр, додекаэдр. Этим фигурам в древности приписывали магические свойстза, они олицетворяли землю, воздух, воду, солнце, космос. Их только пять, больше при всем желании не придумаешь.
Каждая из этих фигур образована одинаковыми равносторонними многоугольниками: треугольниками, квадратами, пятиугольниками. Они и являются основой для построения любых звездчатых многогранников.
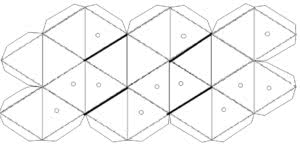
На рисунках 1—5 изображены пять простых многогранников: тетраэдр, гексаэдр, октаэдр, икосаэдр, додекаэдр. Здесь же даны чертежи их граней и возможные варианты разверток для их склейки. Такие грани довольно просто построить, зная основы геометрии.
Элементы для построения звездчатых фигур в основном такие же, только здесь каждая звезда может состоять и из разных граней (см. стр. 16).
Например, фигуры 6, 7, 8 составлены из одинаковых граней, а вот фигуры 9 и 10 — из двух видов граней. Из нескольких граней можно склеить заготовку для одной из вершин звезды, а после соединить их. Чаще всего грани образованы треугольниками либо квадратами. Сложнее форма граней, показанных на рисунках 8, 9, 10.
По приведенным здесь разверткам получится одна из вершин звезды. Остальные делаются так же.
У звезд 6, 7 и 8 все грани для одной заготовки одинаковы. У звезд 9 и 10 по две формы заготовок и, естественно, две формы вершин.
При изготовлении звезд по рисункам 9 и 10 вы убедитесь, что они получаются из взаимного пересечения двух видов более простых звезд. Так, звезда на рисунке 9 составлена из звезд 6 и 7; а звезда на рисунке 10 — из звезд 7 и 8-
Для изготовления звезд лучше всего применять тонкий цветной картон, наборы которого продаются в магазинах канцтоваров. Можно использовать плотную ватманскую бумагу, отходы от упаковок из картона. Для склеивания применяйте клей ПВА.
Из инструментов вам понадобятся: металлическая линейка, остро заточенный твердый карандаш, шило, чертилка или запиленный под шило гвоздь, вставленный в цанговый карандаш, кисть или тонкая вязальная спица для нанесения клея, ножницы прямые с острыми концами, большие и маленькие, и подкладка из картона, на которой вы будете работать.
Из плотной бумаги или картона сначала изготовьте шаблон одной грани, а лучше — заготовки целиком. С приведенных на наших рисунках разверток переколите их контуры. На изнаночной стороне картона соедините метки карандашом, а потом проведите по полученным линиям кончиком шила.
У каждой заготовки оставьте припуск (клапан) для склейки заготовок по ребрам. Согните заготовки по линиям сгиба на лицо, используя линейку.
Изготовиз полный комплект заготовок, приступайте к склейке вершин. Сначала нужно склеить каждую вершину отдельно. Клей наносится на края граней и на оставленный клапан, детали плотно прижимаются друг к другу до высыхания. После этого можно раскрасить одинаковые вершины. Причем у звезд 9 и 10 вершины разной формы должны быть разного цвета.
Для окончательной сборки звезды осталось склеить вершины друг с другом. При этом некоторые клапаны окажутся лишними, их обрезают. Клеить надо так, чтобы все клапаны оказались внутри. Если развертка выкроена правильно, каждая вершина точно встает на свое место. Трудно бывает приклеить последнюю вершину, но подумав, вы найдете выход из положения.
На этом можно было бы и закончите статью. Но все-таки хочется не ограничиваться рекомендациями, с которыми вы познакомились выше. Попробуйте придумать свою звезду! Какой она получится, посмотрим. Ждем от вас сообщений.
А. БИРЮКОВ, г. Курск Рисунки М. СИМАКОВА
15
■
Характеристики
Ромбический додекаэдр — это зоноэдр . Его многогранный двойник — кубооктаэдр . Длина длинной диагонали лица ровно √ 2 раза больше длины диагонали короткой стороны; таким образом, углы на каждой грани измеряют arccos (13), или примерно 70,53 °.
Будучи двойственным к архимедову многограннику , ромбический додекаэдр является гранно-транзитивным , что означает, что группа симметрии твердого тела транзитивно действует на его множестве граней. В элементарных терминах это означает, что для любых двух граней A и B существует вращение или отражение твердого тела, в результате чего оно занимает одну и ту же область пространства при перемещении грани A к грани B.
Ромбический додекаэдр можно рассматривать как выпуклую оболочку объединения вершин куба и октаэдра. 6 вершин, где встречаются 4 ромба, соответствуют вершинам октаэдра , а 8 вершин, в которых встречаются 3 ромба, соответствуют вершинам куба .
Ромбический додекаэдр — один из девяти реберно-транзитивных выпуклых многогранников, остальные — пять Платоновых тел , кубооктаэдр , икосододекаэдр и ромбический триаконтаэдр .
Ромбический додекаэдр можно использовать для мозаики трехмерного пространства: его можно сложить, чтобы заполнить пространство, так же, как шестиугольники заполняют плоскость.
Этот многогранник в пространстве заполнения тесселяции можно рассматривать как Вороную тесселяцию в гранецентрированной кубической решетке . Это зона Бриллюэна объемно-центрированных кубических (ОЦК) кристаллов. Некоторые минералы, такие как гранат, образуют ромбический додекаэдрический кристалл . Как отметил Иоганн Кеплер в своей книге о снежинках 1611 года ( Strena seu de Nive Sexangula ), медоносные пчелы используют геометрию ромбических додекаэдров для формирования сот из мозаики ячеек, каждая из которых представляет собой шестиугольную призму, покрытую половиной ромбического додекаэдра. Ромбический додекаэдр также встречается в элементарных ячейках алмаза и алмазоидов . В этих случаях четыре вершины (чередующиеся тройные) отсутствуют, но химические связи лежат на остальных ребрах.
График ромбического додекаэдра негамильтонов .
Ромбический додекаэдр можно разрезать на четыре тупых треугольных трапеции вокруг его центра. Эти ромбоэдры являются ячейками треугольных трапециевидных сот . Аналогия: правильный шестиугольник можно разрезать на 3 ромба вокруг его центра. Эти ромбы представляют собой плитки ромбика .
В коллекциях Лувра есть матрица в форме ромбического додекадрона, датируемая Птолемеевым Египтом . Грани начертаны греческими буквами, представляющими числа от 1 до 12: Α Β Γ Δ Ε Ζ Ϛ Η Θ Ι ΙΑ ΙΒ. Функция матрицы неизвестна.
Додекаэдр как сделать
Одной из простейших бумажных кусудам считается додекаэдр-оригами. Но это не значит, что он выглядит неэффектно, особенно когда речь идёт о звёздчатой разновидности.
Декоративный многогранник, подобно другим своим родственникам – кусудамам, отлично подходит для праздничного украшения помещений или в качестве оригинального подарка.
Мини-додекаэдры можно использовать как модные украшения, сделав из них серьги или кулон.
Как сделать объемные геометрические фигуры
Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.
Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.
Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.
Схемы для вырезания
Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.
Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).
Шара
Выкройка шара состоит из 8 частей, 12, 16 или большего количества. Присутствуют и другие способы изображения мяча. Например, из 6 деталей или 4 широких клиньев.
Материал, из чего можно сделать плотный шар — картон или плотная бумага.
Шаблоны для склеивания
Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.
Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.
https://youtube.com/watch?v=BP50HPyEuKY
Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.
Макеты из бумаги
Макетирование — увлекательное занятие. Оно помогает развить воображение и логическое мышление. Из бумаги делают не только фигуры, но и необычные скульптуры, статуэтки, шестиугольные–двенадцатиугольные предметы, наклонные объекты (например, Пизанскую башню), карандаши, линейки. На фото и картинках можно посмотреть, как выглядят оригинальные поделки из бумаги.
Школьники младших классов или дошколята делают бумажные объемные поделки. Например, предметы из овала — веер, цветы, гусеницы. Для них потребуются овалы и круги разного диаметра. Раскладки склеиваются между собой, получаются трехмерные игрушки.
Применяется множество вариантов, как сделать кораблик из бумаги.
Простая схема.
Как вырезать и склеить модели из бумаги
Начинающие конструкторы задаются вопросами, как рисовать и чертить геометрические фигуры, как правильно склеить выкройки и как делают врезки. Проще всего распечатать готовый шаблон. Затем необходимо согнуть фигуру по пунктирным линиям.
Чтобы сгибы получились ровными, к пунктиру прикладывают линейку, по ее форме делают точные загибы. Такой способ особенно помогает, когда речь идет о фигурках из картона или ребенок делает самые сложные макеты. Например, икосаэдр, додекаэдр, тетраэдр.
На последнем этапе необходимо скрепить элементы объекта, места для склейки обозначены на развернутом виде фигуры. Детали из картона приклеивают при помощи ПВА, а бумажные — карандашным клеем.
Основные ошибки при работе с моделями:
Ребенок делает неправильные сгибы — например, изгиб отклоняется в сторону от пунктира на несколько градусов. В результате модель получится неточной.
Неточности во время вырезания шаблонов. Если малыш отрезал одну из границ для склеивания, то фигурка будет разворачиваться. Здесь на помощь придет взрослый.
Kak sdelat origami kolyuchiy ikosododekaedr polnaya instrukciya po skladyvaniyu
Икосаэдр из бумаги. Чертёж развертки икосаэдра.Подробнее
DIY — Как сделать ДВУХКЛИНКОВУЮ ГЛЕФУ из бумаги а4 своими руками?Подробнее
How to make an Origami Spiky Icosidodecahedron (Complete Folding Instructions)Подробнее
Девятая звёздчатая форма икосаэдра. Сборка многогранника своими рукамиПодробнее
Звездчатый многогранник из соединения четырех тетраэдровПодробнее
Красивый многогранник из бумаги своими рукамиПодробнее
3D дикобраз! Инструкция по сборке картонной фигуры.Подробнее
Как сделать Простой VS Сложный Пистолет из ЛЕГОПодробнее
КАК СДЕЛАТЬ ТАТУ МАШИНКУ? | БЬЕМ ТАТУ НА ПАЦАНЕПодробнее
Геометрические отношения
Додекаэдра является третьим в бесконечном множестве усеченного trapezohedra которая может быть построена путем усечения двух осевых вершин пятиугольного трапецоэдра .
В созвездиях регулярного додекаэдра составляют три из четырех Кеплер-Пуансо многогранников .
Выпрямляются додекаэдр образует икосододекаэдр .
Правильный додекаэдр имеет икосаэдрическую симметрию I h , группу Кокстера , порядок 120, с абстрактной групповой структурой A 5 × Z 2 .
Отношение к правильному икосаэдру
Когда правильный додекаэдр вписан в сферу , он занимает больше объема сферы (66,49%), чем икосаэдр, вписанный в ту же сферу (60,55%).
Правильный додекаэдр с длиной ребра 1 имеет более чем в три с половиной раза объем икосаэдра с такой же длиной ребер (7,663 … по сравнению с 2,181 …), что примерно составляет 3,512 461 179 75 , или в точных терминах:35(3 ϕ + 1) или (1,8 ϕ + 0,6) .
У правильного додекаэдра 12 граней и 20 вершин, а у правильного икосаэдра 20 граней и 12 вершин. У обоих по 30 ребер.
Отношение к вложенному кубу
Куб может быть встроен в правильный додекаэдр, прикрепленный к восьми из его равноудаленных вершин в пяти различных положениях. Фактически, пять кубов могут перекрываться и сцепляться внутри правильного додекаэдра, в результате чего получается соединение пяти кубов .
Отношение ребра правильного додекаэдра к ребру куба, вложенного внутрь такого правильного додекаэдра, равно 1: ϕ или ( ϕ — 1): 1.
Отношение объема правильного додекаэдра к объему куба, заключенного внутри такого правильного додекаэдра, равно 1: 22 + ϕ, или 1 + ϕ2 : 1 или (5 + √ 5 ): 4.
Например, вложенный куб с объемом 64 (и длиной ребра 4) будет вложен в правильный додекаэдр объемом 64 + 32 ϕ (и длиной ребра 4 ϕ — 4).
Таким образом, разница в объеме между окружающим правильным додекаэдром и замкнутым кубом всегда равна половине объема куба, умноженного на ϕ .
Из этих соотношений выводятся простые формулы для объема правильного додекаэдра с длиной ребра a через золотую середину:
- V = ( aϕ ) 3 ·14(5 + √ 5 )
- V =14(14 ϕ + 8) а 3
Отношение к золотому прямоугольнику
Золотые прямоугольники отношения ( ϕ + 1): 1 и ϕ : 1 также идеально вписываются в правильный додекаэдр. Пропорционально этому золотому прямоугольнику край замкнутого куба равен ϕ , когда большая длина прямоугольника равна ϕ + 1 (или ϕ 2 ), а короткая длина равна 1 (ребро, общее с правильным додекаэдром).
Кроме того, в центре каждой грани правильного додекаэдра образуют три пересекающихся золотых прямоугольника.
Связь с 6-кубом и ромбическим триаконтаэдром
Проекция 6-полукуба на правильную додекаэдрическую огибающую
Его можно спроецировать в 3D из 6-мерного 6-полукуба, используя те же базисные векторы, которые образуют оболочку из 6-куба . Показанные здесь 12 внутренних вершин, которые не соединены ребрами внешней оболочки с 6D нормальной длиной √ 2 , образуют правильный икосаэдр .
Используемые базисные векторы трехмерной проекции [ u , v , w ]:
- u = (1, ϕ , 0, −1, ϕ , 0)
- v = ( ϕ , 0, 1, ϕ , 0, −1)
- w = (0, 1, ϕ , 0, −1, ϕ )
Габаритные размеры
Обозначив a длину ребра ромбического додекаэдра,
радиус его вписанного шара ( касательной к каждой из граней ромбического додекаэдра в) является
- рязнак равно63 а≈0,8164965809 а{\ displaystyle r _ {\ mathrm {i}} = {\ frac {\ sqrt {6}} {3}} ~ a \ приблизительно 0,816 \, 496 \, 5809 ~ a \ quad}( OEIS : A157697 ),
радиус его средней сферы составляет
- рмзнак равно223 а≈0,94280904158 а{\ displaystyle r _ {\ mathrm {m}} = {\ frac {2 {\ sqrt {2}}} {3}} ~ а \ приблизительно 0,942 \, 809 \, 041 \, 58 ~ а \ quad}( OEIS : A179587 ),
радиус сферы, проходящей через шесть вершин четвертого порядка, но не через восемь вершин третьего порядка, равен
- рознак равно233 а≈1.154700538 а{\ displaystyle r _ {\ mathrm {o}} = {\ frac {2 {\ sqrt {3}}} {3}} ~ а \ приблизительно 1.154 \, 700 \, 538 ~ а \ quad}( OEIS : A020832 ),
радиус сферы, проходящей через восемь вершин порядка 3, в точности равен длине сторон
- ртзнак равноа{\ Displaystyle г _ {\ mathrm {т}} = а}
Ажурная модель
Существует несколько типов оригами-додекаэдров, но сделать эту прозрачную конструкцию из бумажных модулей проще всего. Хорошее задание для детей, желающих познакомиться с азами пространственной геометрии и взрослых, ищущих эффективное средство для снятия стресса. Желательно использовать для игрушки бумагу ками с рисунком, она придаст особый шарм и колорит.
Пошаговая инструкция:
- Для создания кусудамы понадобится 30 одинаковых модулей. Их складывают из прямоугольников, имеющих соотношение сторон 3:4. Например, размером 6х8 см, 9х12 см и так далее. Можно брать как одно-, так и двухсторонние листы.
- Складываем каждый прямоугольник пополам вдоль длинной стороны. После чего делаем Z-образный сгиб.
- Располагаем получившуюся полоску длинной стороной к себе. Загибаем правый нижний угол вверх. Переворачиваем заготовку на 180°. И повторяем действие для правого нижнего угла (другого).
- Складываем фигуру по диагонали, как показано на рис 4.
- Модули для додекаэдра-кусудамы готовы.

Остаётся соединить их в пространственную композицию. Для этого короткую часть одного модуля вставляем к «карман» длинной части другого. И располагаем так, чтобы внутренние углы и грани обоих элементов совпали.

Аналогичный образом добавляем третий модуль, соединяя его с предыдущими двумя и формируя устойчивый конструктивный узел.

Продолжаем крепить детали друг к другу, пока не получится объёмная фигура.

За счёт необычной бумаги с принтом, получается стильный предмет декора. Чтобы кусудама не распадалась, лучше соединить узловые элементы с помощью клея.

Подробная сборка ажурного додекаэдра представлена и в видео-МК:
https://youtube.com/watch?v=ZBiB7233jA8
Разнообразие фигур
На основе пяти приведенных видов, используя умение и фантазию, умельцы легко конструируют множество различных моделей из бумаги. Многогранник может совершенно отличаться от вышеописанных пяти фигур, формируясь одновременно из различных по форме граней, например из квадратов и треугольников. Так получаются архимедовы тела. А если одну или несколько граней пропустить, то получится открытая фигура, просматриваемая как снаружи, так и внутри. Для изготовления объемных моделей используются специальные выкройки, вырезаемые из достаточно плотной, хорошо держащей форму, бумаги. Делают и особенные многогранники из бумаги. Схемы таких изделий предусматривают наличие дополнительных, выступающих модулей. Разберем способы, как сконструировать очень красивую фигуру на примере додекаэдра (фото 3).
Разузнай! – Додекаэдр – Как сделать правильный додекаэдр своими руками – Как сделать звездчатый додекаэдр – Разузнай!
Додекаэдром называется правильный многогранник, составленный из двенадцати правильных пятиугольников. Эта эффектная объемная фигура обладает центром симметрии, называемым центром додекаэдра.
Кроме того, в ней присутствуют пятнадцать плоскостей симметрии (в каждой грани любая из них проходит через середину противоположного ребра и вершину) и пятнадцать осей симметрии (пересекающих середины параллельных противолежащих ребер).
Каждая из вершин додекаэдра является вершиной трех пятиугольников правильной формы.
Свое название конструкция получила по количеству входящих в нее граней (традиционно древние греки давали многогранникам имена, отображающие число граней, составляющих структуру фигуры). Таким образом, понятие «додекаэдр» образовано из значений двух слов: «додека» (двенадцать) и «хедра» (грань).
Фигура относится к одному из пяти Платоновых тел (наряду с тетраэдром, октаэдром, гексаэдром (кубом) и икосаэдром).
Интересно, что согласно многочисленным историческим документам, все они активно использовались жителями Древней Греции в виде настольных игральных костей и изготавливались из самого различного материала.
Правильные многогранники всегда привлекали людей своей красотой, органичностью и необыкновенным совершенством форм, но додекаэдр имеет особую историю, которая из года в год обрастает все новыми, иногда совершенно мистическими, фактами.
Представители многих цивилизаций усматривали в нем сверхъестественную и таинственную сущность, утверждая, что: «Из числа двенадцать произрастает многое». На территориях древних разрушенных государств до сих пор находят маленькие фигурки в виде додекаэдров, выполненные из бронзы, камня или кости.
Кроме того, при раскопках на землях современной Англии, Франции, Германии, Венгрии, Италии археологи обнаружили несколько сотен так называемых «римских додекаэдров», датирующихся II-III-м веками нашей эры. Основные размеры фигурок составляют от четырех до одиннадцати сантиметров, причем отличаются они самыми невероятными узорами, текстурами и техникой исполнения.
Как сделать правильный додекаэдр своими руками
Сегодня конструкция данной фигуры нашла свое отображение во многих вариантах художественного творчества, архитектуре и строительстве.
Народные умельцы изготавливают из цветной или белой бумаги необыкновенные по красоте оригами в виде ажурных додекаэдров, а из картона делают оригинальные и прочее).
В продаже можно приобрести уже готовые наборы, содержащие все необходимое для изготовления сувениров, но наиболее интересно произвести весь процесс работы своими руками, начиная от построения отдельных деталей и заканчивая сборкой готовой конструкции.
Для того, чтобы сделать правильный додекаэдр из картона, необходим собственно сам материал и подручные средства:
- ножницы,
- карандаш,
- ластик,
- линейка,
- клей.
Хорошо иметь тупой нож или какое-либо приспособление для загибания припусков, но если их нет, то вполне подойдет металлическая линейка или те же ножницы.
Делаем правильный додекаэдр
-
- Самый первый этап в изготовлении – построение пятиугольника нужного размера. Должен получиться вот такой элемент. Он и станет основой фигуры.
- Далее конструируете развертку додекаэдра с учетом припусков на склеивание.
В результате получится «выкройка» приблизительно такого вида. Варианты могут различаться, если припуски будут другой формы или размещены на других гранях.
- Аккуратно по линиям сгибаете припуски.
- Склеиваете.
- Наносите на готовый додекаэдр нужный рисунок или декорируете другим выбранным способом.
Готово!
Как сделать звездчатый додекаэдр
Звездчатые додекаэдры имеют более сложную конструкцию по сравнению с обычными. Эти многогранники подразделяются на малый (первого продолжения), средний (второго продолжения) и большой (последняя звездчатая форма правильного додекаэдра). Каждый из них отличается своими особенностями построения и сборкой.
Для работы Вам потребуются те же материалы и инструменты, что и для изготовления стандартного додекаэдра.
Если Вы решили сделать первый вариант (малый додекаэдр), то необходимо построить чертеж первого элемента, который станет основой для всей конструкции (в дальнейшем производится ее склеивание или сборка деталей при помощи скрепок).
Делаем звездчатый додекаэдр
- Строите схему основной детали нужных размеров с необходимыми припусками. Должен получиться приблизительно такой элемент.
- По обозначенным линиям сгибаете, в том числе не забываете о припусках.
- Склеиваете каждую деталь по отдельности.
- Собираете додекаэдр полностью.
- Раскрашиваете или наносите любое из выбранных изображений.
Готово!
Связанные многогранники и мозаики
Правильный додекаэдр топологически связан с серией мозаик вершиной n 3 .
| * n 32 изменение симметрии правильных мозаик: { n , 3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Сферический | Евклидово | Компактная гиперболия. | Paraco. | Некомпактный гиперболический | |||||||
| {2,3} | {3,3} | {4,3} | {5,3} | {6,3} | {7,3} | {8,3} | {∞, 3} | {12i, 3} | {9i, 3} | {6i, 3} | {3i, 3} |
Правильный додекаэдр может быть преобразован последовательностью усечения в его двойственный икосаэдр:
| Семейство однородных икосаэдрических многогранников | |||||||
|---|---|---|---|---|---|---|---|
| Симметрия : , (* 532) | + , (532) | ||||||
| {5,3} | т {5,3} | г {5,3} | т {3,5} | {3,5} | рр {5,3} | tr {5,3} | ср {5,3} |
| Двойники к однородным многогранникам | |||||||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
| Симметрия : , (* 432) | + (432) | = (* 332) | (3 * 2) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| {4,3} | т {4,3} | г {4,3} г {3 1,1 } | т {3,4} т {3 1,1 } | {3,4} {3 1,1 } | rr {4,3} s 2 {3,4} | tr {4,3} | sr {4,3} | ч {4,3} {3,3} | ч 2 {4,3} т {3,3} | с {3,4} с {3 1,1 } |
| знак равно | знак равно | знак равно | знак равно или | знак равно или | знак равно | |||||
| Двойники к однородным многогранникам | ||||||||||
| V4 3 | V3.8 2 | В (3,4) 2 | V4.6 2 | V3 4 | V3.4 3 | V4.6.8 | V3 4 .4 | V3 3 | V3.6 2 | V3 5 |
Правильный додекаэдр является членом последовательности неоднородных многогранников и мозаик, составленных из пятиугольников с конфигурациями граней (V3.3.3.3. N ). (При n > 6 последовательность состоит из мозаик гиперболической плоскости.) Эти транзитивные по граням фигуры обладают ( n 32) симметрией вращения .
| n 32 мутации симметрии курносых мозаик: 3.3.3.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия n 32 | Сферический | Евклидово | Компактный гиперболический | Paracomp. | ||||
| 232 | 332 | 432 | 532 | 632 | 732 | 832 | ∞32 | |
| Курносые фигуры | ||||||||
| Конфиг. | 3.3.3.3.2 | 3.3.3.3.3 | 3.3.3.3.4 | 3.3.3.3.5 | 3.3.3.3.6 | 3.3.3.3.7 | 3.3.3.3.8 | 3.3.3.3.∞ |
| Гироскопические фигуры | ||||||||
| Конфиг. | V3.3.3.3.2 | V3.3.3.3.3 | V3.3.3.3.4 | V3.3.3.3.5 | V3.3.3.3.6 | V3.3.3.3.7 | V3.3.3.3.8 | V3.3.3.3.∞ |
Красивая геометрия
Украшать интерьер дома, создавая своими руками необычные, стильные вещи, — это увлекательное творчество. Смастерить самостоятельно из плотной бумаги различные многогранники — значит создать уникальные вещи, которые могут стать просто занятием на день или два, а могут превратиться в дизайнерские интерьерные украшения. К тому же с развитием техники, способной к пространственному моделированию всевозможных вещей, стало возможным создание стильных и современных 3D-моделей. Есть мастера, которые при помощи простроения разверток по законам геометрии делают из бумаги макеты животных и различных предметов. Но это достаточно сложное математическое и чертежное творчество. Начать работать в подобной технике поможет
Что такое тетраэдр
С помощью наглядной объемной фигуры детям проще научиться иметь представление о пространственном мышлении. В этом помогут объемные геометрические фигуры, сделанные своими руками из бумаги. Тетраэдр представляет собой многоугольную фигуру, которая считается простейшей. Он состоит из 4-х граней, каждая из них является равносторонним треугольником. Стороны треугольников соединяются между собой только одной гранью. В фигуре есть также четыре вершины и шесть ребер.
Людей с давних пор привлекали многогранники как удивительные символы симметрии. Они считали их божественными фигурами. Эти фигуры очень важны в развитии математического мышления детей дошкольного и школьного возраста. Они способствуют развитию геометрического представления и пространственного мышления.
На самом деле такая фигура встречается нам повсюду. Однако, сразу ее заметить сложно. Выполненная из стержней, она встречается как основа для пространственных конструкций:
- мостов;
- перекрытий;
- балок;
- ферм;
- пролетов зданий.
Для того чтобы получить такую фигуру, можно не прибегать к сложным математическим вычислениям. Полученная модель позволит иметь наглядное представление о свойствах геометрической фигуры в объемном изображении.
Как сделать многогранник из бумаги: второй способ
Изготовьте два главных шаблона (фото 5):
— Первый.
Нарисуйте на листе окружность и поделите ее поперек на две части. Одна будет основой для выкройки, дугу второй сразу сотрите для удобства. Поделите деталь на пять равных частей и ограничьте все радиусы поперечными отрезками. В результате получатся соединенные вместе пять одинаковых равнобедренных треугольников. Изобразите рядом примыкающую к среднему отрезку точно такую же полуокружность, только в зеркальном отражении. Полученная деталь при сворачивании выглядит как два конуса. Изготовьте таких аналогичных шаблонов всего шесть штук. Для их склеивания используется вторая деталь, которая будет помещаться вовнутрь.
— Второй.
Этот шаблон — пятиконечная звезда. Выполните одинаковые двенадцать заготовок. Формируя многогранник, каждую из звезд с подогнутыми вверх концами помещают внутрь конусообразных деталей и приклеивают к граням.
Полный сбор фигуры получается путем соединения двойных блоков дополнительными отрезками бумаги, заводя их вовнутрь. Моделируя изделия, довольно проблематично сделать их разными по размеру. Готовые модели многогранников из бумаги не так-то просто увеличить. Для этого недостаточно просто сделать припуски по всем внешним границам. Нужно масштабировать отдельно каждую из граней. Только так возможно получить увеличенную копию первоначальной модели. Используя второй способ изготовления многогранника, сделать это намного проще, так как будет достаточно увеличить первоначальные заготовки, по которым уже выполняется нужное количество отдельных деталей.
Как сделать многогранник?
Необходимость сделать многогранник возникает нечасто, однако случается, что ребёнку на дом задают это задание или вы решаете сделать оригинальный подарок другу. А возможно, у вас возникла какая-то дизайнерская задумка. Так или иначе, понадобился многогранник из бумаги. Как его склеить?
Современное использование додекаэдра
В настоящее время геометрические объекты в форме додекаэдра находят применение в некоторых сферах деятельности человека:
Игральные кости для настольных игр. Так как додекаэдр — это платоновская фигура, обладающая высокой симметрией, то объекты этой формы можно использовать в играх, где продолжение событий имеет вероятностный характер. Игральные кости в своем большинстве изготавливают кубической формы, поскольку их сделать проще всего, однако современные игры становятся все сложнее и разнообразнее, а значит, требуют костей с большим количеством возможностей. Кости в форме додекаэдра применяются в ролевой настольной игре Dungeons and Dragons. Особенностью этих костей является то, что сумма цифр, расположенных на противоположных гранях, всегда равна 13.
Источники звука. Современные звуковые колонки часто изготавливают в форме додекаэдра, поскольку они распространяют звук во всех направлениях и защищают его от окружающего шума.
Додекаэдр-звезда
Правильные звёздчатые многогранники относятся к самым красивым геометрическим фигурам. С момента своего открытия в XVI веке, они считались символом совершенства Вселенной. Малый звёздчатый додекаэдр впервые построил немецкий астроном и математик Иоганн Кеплер – создатель знаменитой теории о строении Солнечной системы. Многогранник имеет собственное имя: Арур Кэли, в честь английского учёного, сделавшего огромный вклад в развитие линейной алгебры.
Малый звёздчатый додекаэдр-оригами представляет собой фигуру из 12 граней-пентаграмм, с пятью пентаграммами, сходящимися к вершинам. Он состоит из 30 модулей, которые складываются из квадратов, размером 8х8 см. Лучше всего использовать профессиональную бумагу-оригами, которая позволит создавать чёткие грани и жёсткие узлы, не позволяющие конструкции распадаться или деформироваться.
https://youtube.com/watch?v=KQ6omSCOwsc
Практическое использование
В компоновке реактивного колеса космического корабля обычно используется четырехгранная конфигурация четырех колес. Для колес, которые работают одинаково (с точки зрения максимального крутящего момента и максимального углового момента) в обоих направлениях вращения и по всем четырем колесам, максимальный крутящий момент и максимальный крутящий момент для 3-осевой системы управления ориентацией (с учетом идеализированных приводов) задаются путем проецирования. тессеракт , представляющий пределы крутящего момента или импульс каждого колеса в 3D пространства через матрицу колесных осей 3 × 4; полученный трехмерный многогранник представляет собой ромбический додекаэдр. Такое расположение реактивных колес — не единственная возможная конфигурация (более простое расположение состоит из трех колес, установленных для вращения вокруг ортогональных осей), но оно дает преимущество в обеспечении избыточности для смягчения отказа одного из четырех колес (с ухудшенными общими характеристиками. доступный с оставшихся трех активных колес) и в обеспечении более выпуклой оболочки, чем куб, что приводит к меньшей зависимости маневренности от направления оси (с точки зрения привода / установки). Массовые характеристики космического корабля влияют на общий импульс и маневренность системы, поэтому уменьшение отклонения границы оболочки не обязательно приводит к увеличению однородности предпочтительных смещений осей (то есть, даже с идеально распределенным пределом характеристик внутри подсистемы исполнительного механизма, предпочтительные оси вращения не обязательно произвольны. на системном уровне).
Делаем двадцатигранник
Икосаэдр состоит из одинаковых по размеру равнобедренных треугольников. Его можно легко сложить, используя представленную на рисунке 2 развертку. Возьмите прямоугольный лист бумаги. Начертите на нем двадцать одинаковых по размеру и форме треугольников, расположив их в четырех рядах. При этом каждая грань одного будет одновременно являться стороной другого. Полученный шаблон используйте для изготовления заготовки. Она будет отличаться от основы-развертки наличием припусков для склеивания по всем внешним линиям. Вырезав из бумаги заготовку, согните ее по линиям. Формируя из бумаги многогранник, замыкайте крайние ряды между собой. При этом вершины треугольников соединятся в одну точку.






