Поделка посложнее
Конус делается немного сложнее. Для начала нарисовать циркулем окружность. Вырезать сектор (часть кружка, ограниченная дугой окружности и двумя радиусами) из этой окружности. Острота конца конуса зависит от вырезанной части большого сектора.
Склеить боковую поверхность конуса. Далее измерить диаметр основания конуса. Циркулем нарисовать окружность на листе бумаги. Затем дорисовать треугольнички для склеивания основы с боковой поверхности. Вырезать. После приклеить основание к боковой поверхности. Поделка готова!
Статья по теме: Подарочная корзина своими руками для мужчины: мастер-класс с фото
Ажурная модель
Существует несколько типов оригами-додекаэдров, но сделать эту прозрачную конструкцию из бумажных модулей проще всего. Хорошее задание для детей, желающих познакомиться с азами пространственной геометрии и взрослых, ищущих эффективное средство для снятия стресса. Желательно использовать для игрушки бумагу ками с рисунком, она придаст особый шарм и колорит.
Пошаговая инструкция:
- Для создания кусудамы понадобится 30 одинаковых модулей. Их складывают из прямоугольников, имеющих соотношение сторон 3:4. Например, размером 6х8 см, 9х12 см и так далее. Можно брать как одно-, так и двухсторонние листы.
- Складываем каждый прямоугольник пополам вдоль длинной стороны. После чего делаем Z-образный сгиб.
- Располагаем получившуюся полоску длинной стороной к себе. Загибаем правый нижний угол вверх. Переворачиваем заготовку на 180°. И повторяем действие для правого нижнего угла (другого).
- Складываем фигуру по диагонали, как показано на рис 4.
- Модули для додекаэдра-кусудамы готовы.

Остаётся соединить их в пространственную композицию. Для этого короткую часть одного модуля вставляем к «карман» длинной части другого. И располагаем так, чтобы внутренние углы и грани обоих элементов совпали.

Аналогичный образом добавляем третий модуль, соединяя его с предыдущими двумя и формируя устойчивый конструктивный узел.

Продолжаем крепить детали друг к другу, пока не получится объёмная фигура.

За счёт необычной бумаги с принтом, получается стильный предмет декора. Чтобы кусудама не распадалась, лучше соединить узловые элементы с помощью клея.

Подробная сборка ажурного додекаэдра представлена и в видео-МК:
https://www.youtube.com/watch?v=ZBiB7233jA8
https://youtube.com/watch?v=YqnT-_QRRbM
https://youtube.com/watch?v=bM2HzLhsVbw
Задание 2 (построение прямоугольного треугольника)
Постройте на нелинованной бумаге треугольник , чтобы угол был прямым, длина стороны равнялась 15 см, а длина сторогы – 20 см.
Построим точку (Рис. 18).
Рис. 18. Точка
Проведем через точку прямую (Рис. 19).
Рис. 19. Прямая, проведенная через точку
Для построения прямого угла воспользуемся прямоугольным треугольником. Приложим треугольник так, чтобы вершина прямого угла совпала с точкой , а одна из сторон совпала с лучом, как показано на рис. 20.
Рис. 20. Построение прямого угла
Проведем по второй стороне прямого угла треугольника луч из точки и получим прямой угол (Рис. 21).
Рис. 21. Полученный прямой угол
Выполним построение сторон треугольника. Построим отрезок , который равен 15 см (Рис. 22).
Рис. 22. Отрезок
Построим отрезок , который равен 20 см (Рис. 23).
Рис. 23. Отрезок
Соединим полученные точки отрезком . Мы получили прямоугольный треугольник (Рис. 24) с прямым углом и сторонами см и см.
Рис. 24. Треугольник
Разнообразие фигур (adsbygoogle = window.adsbygoogle || []).push({});
На основе пяти приведенных видов, используя умение и фантазию, умельцы легко конструируют множество различных моделей из бумаги. Многогранник может совершенно отличаться от вышеописанных пяти фигур, формируясь одновременно из различных по форме граней, например из квадратов и треугольников. Так получаются архимедовы тела. А если одну или несколько граней пропустить, то получится открытая фигура, просматриваемая как снаружи, так и внутри. Для изготовления объемных моделей используются специальные выкройки, вырезаемые из достаточно плотной, хорошо держащей форму, бумаги. Делают и особенные многогранники из бумаги. Схемы таких изделий предусматривают наличие дополнительных, выступающих модулей. Разберем способы, как сконструировать очень красивую фигуру на примере додекаэдра (фото 3).
Бумажная модель
Используя 30 квадратных листов бумаги (размер каждой стороны 7,5 см), можно сделать довольно крепкую версию одной из разновидности этого геометрического чуда совсем без склеивания. Если в запасе есть материал разного цвета, то получится яркий и красивый макет с разноцветными блоками. Инструкция по изготовлению звездчатого икосаэдра поэтапно:

- Сложить листок пополам и сделать складку вдоль сгиба. Если используется бумага для оригами, то стоит убедиться, что её лицевая сторона находится снаружи, поскольку она будет видна позже.
- Развернуть квадрат.
- Сложить правую и левую стороны листа так, чтобы они встретились в месте сгиба. Должен получиться прямоугольник, больше похожий на шкаф с распашными дверцами.
- Перевернуть фигуру подогнутыми краями вниз.
- Сделать диагональную складку: верхний правый угол должен встретиться с левой стороной прямоугольника. Нужно свернуть обе «двери шкафа».
- Перевернуть бумагу прямым концом вверх.
- Сделать ещё одну диагональную складку, где верхний правый угол будет встречаться со стороной макета. Должен получиться параллелограмм.
- Согнуть лист по диагонали там, где верхний угол соответствует правому углу фигуры.
- Повторить действие с другой стороны. Должны встретиться нижний и левый углы. Получится маленький квадрат.
- Затем повернуть заготовку так, чтобы фигура напоминала ромб.
- Сложить квадрат пополам, сделав сгиб, который идёт перпендикулярно «дверцам шкафа», видимым на модели. Итак, первая единица готова.
Всего таких блоков нужно сделать 30. Например, по 10 разного цвета.
Модели для 5 класса
Десятилетним подросткам предлагаются сложные схемы, часто включающие несколько этапов складывания. В первую очередь акцент делается на классическом модульном оригами – кусудамах и многогранниках из нескольких одинаковых частей. Также можно изготавливать функциональные изделия: бижутерию, коробочки, закладки для книг, светильники, панно на стену, ёлочные игрушки и так далее.
Простая цветочная кусудама
Кусудама – это бумажный шар, используемый как интерьерное украшение. Прежде он играл роль подвесного саше и наполнялся ароматическими травами для санации воздуха. Самая простая кусудама – цветочная. Она состоит из 6-лепестковых лилий, собираемых модульным способом.

Очень красиво смотрятся подобные кусудамы, выполненные из бумаги «ками» с разными узорами. Можно использовать и листы старых глянцевых журналов, нотные тетради или календари. В Японии ажурные бумажные шары считались оберегом и в этом качестве их можно дарить близким людям и друзьям.
Пошаговая инструкция:
Потребуется 6 квадратов бумаги любого размера – чем они будут больше, тем объёмнее в итоге получится шар. Однако и плотность листов должна соответственно увеличиваться. Стандартным считается размер 15х15 см.
- Лист сгибаем по диагонали. Это базовая складка «Треугольник» («Косынка), с которой часто начинается изготовление фигур-оригами.
- Правый и левый угол заготовки поднимаем, совмещая с верхней точкой. Обе половины располагаем вдоль центральной линии. Хорошо проглаживаем складки стеком или линейкой, чтобы они получились чёткими и ровными. От этого зависит внешний вид цветка.
- Обе половины верхнего слоя заготовки отгибаем в стороны, совмещая с краями фигуры.
- Раскрываем только что сделанные «карманы». Этот приём в оригами называется «сквош-фолд». Верхние треугольники с обеих сторон опускаем вниз.

Обе складки «сквош-фолд» сгибаем пополам и склеиваем боковины между собой. Получается один лепесток нашей лилии.

Изготавливаем ещё 5 аналогичных деталей. Остаётся последовательно скрепить их между собой.
Для этого подойдёт горячий клей или «Момент Кристалл». Чтобы стороны не расходились, их на время высыхания скрепляют прищепкой или скрепкой.

Можно сделать лилию однотонной, собрав кусудаму из нескольких контрастных или нюансных оттенков. Либо добавить узорчатые лепестки.

Для шара среднего размера потребуется 12 цветков.

Сборку начинаем с двух половинок. Соединяем по 6 лилий. Клеем промазываем тыльные стороны соседних лепестков на одном цветке, то же делаем на втором и прикладываем их друг к другу точно, без сдвигов. Фиксируем до высыхания прищепками.

5 лилий образуют круг с общим центром.
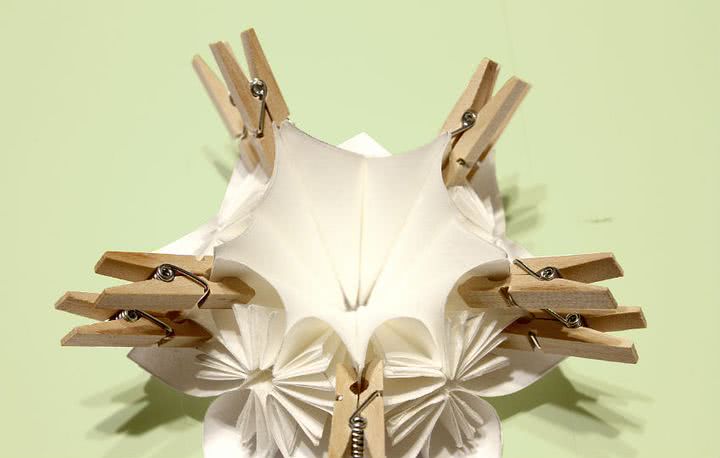
Последнюю – шестую, вклеиваем в середину.

Соединяем две половинки и оставляем на ночь до полного высыхания. Если применяется термопистолет, ждать не нужно.

Кусудама готова. Шары-оригами часто изготавливают на предусмотренных ФГОС «внеурочках» в 5-м классе, особенно во время подготовки к Новому году или другим праздникам. Чтобы изделие приобрело более аккуратный и декоративный вид, центр каждой лилии украшают пуговицами, деталями для скрапбукинга, стразами и так далее. Можно добавить декоративные шнуры и сделать подвески.


Но цветы кусудамы применяются не только в шарах. Если закрепить их на флористическую проволоку, можно собрать невероятно модный сегодня букет невесты в стиле «хенд-мейд».

Ещё один вариант очень красивой цветочной кусудамы, показательной с точки зрения геометрических построений. Для неё понадобится 30 прямоугольников, размером 7х11,5 см. Одна деталь представляет собой один модуль.
https://youtube.com/watch?v=SbxJvdRnbxk
Как сделать геометрические фигуры из бумаги? Схемы и советы
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
- капризный, хрупкий материал
- требует высокой аккуратности, внимательности, усидчивости при работе
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Вам понадобятся следующие материалы:
- лист бумаги
- карандаш
- линейка
- ластик
- ножницы
- клей ПВА либо клеящий карандаш
- кисточка для клея, лучше из жесткой щетины
- циркуль (для некоторых фигур)
Правильные и неправильные звездчатые многогранники
Складывая платоновые тела между собой в определенном порядке, вы можете построить немало звездчатых многоранников — красивых, сложных, многокомпонентных. Но они будут называться «неправильными звездчатыми многогранниками». Правильных звездчатых многогранников всего четыре: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Развертки многогранников для склеивания не будут простыми чертежами. Они, как и фигуры, будут состоять из нескольких компонентов. Так, например, малый звездчатый додекаэдр строится из 12 пятиугольных равнобочных пирамид, сложенных по типу правильного додекаэдра. То есть для начала придется начертить и склеить 12 одинаковых штук правильных пирамид, состоящих из 5 равных граней. И только затем из них можно сложить звездчатый многогранник. Развертка самого малого звездчатого додекаэра — сложное и практически невыполнимое задание. Чтобы ее простроить, нужно суметь на одной плоскости уместить соединенные друг с другом 13 разверток разных геометрических объемных тел.
Характеристики
Ромбический додекаэдр — это зоноэдр . Его многогранный двойник — кубооктаэдр . Длина длинной диагонали лица ровно √ 2 раза больше длины диагонали короткой стороны; таким образом, углы на каждой грани измеряют arccos (13), или примерно 70,53 °.
Будучи двойственным к архимедову многограннику , ромбический додекаэдр является гранно-транзитивным , что означает, что группа симметрии твердого тела транзитивно действует на его множестве граней. В элементарных терминах это означает, что для любых двух граней A и B существует вращение или отражение твердого тела, в результате чего оно занимает одну и ту же область пространства при перемещении грани A к грани B.
Ромбический додекаэдр можно рассматривать как выпуклую оболочку объединения вершин куба и октаэдра. 6 вершин, где встречаются 4 ромба, соответствуют вершинам октаэдра , а 8 вершин, в которых встречаются 3 ромба, соответствуют вершинам куба .
Ромбический додекаэдр — один из девяти реберно-транзитивных выпуклых многогранников, остальные — пять Платоновых тел , кубооктаэдр , икосододекаэдр и ромбический триаконтаэдр .
Ромбический додекаэдр можно использовать для мозаики трехмерного пространства: его можно сложить, чтобы заполнить пространство, так же, как шестиугольники заполняют плоскость.
Этот многогранник в пространстве заполнения тесселяции можно рассматривать как Вороную тесселяцию в гранецентрированной кубической решетке . Это зона Бриллюэна объемно-центрированных кубических (ОЦК) кристаллов. Некоторые минералы, такие как гранат, образуют ромбический додекаэдрический кристалл . Как отметил Иоганн Кеплер в своей книге о снежинках 1611 года ( Strena seu de Nive Sexangula ), медоносные пчелы используют геометрию ромбических додекаэдров для формирования сот из мозаики ячеек, каждая из которых представляет собой шестиугольную призму, покрытую половиной ромбического додекаэдра. Ромбический додекаэдр также встречается в элементарных ячейках алмаза и алмазоидов . В этих случаях четыре вершины (чередующиеся тройные) отсутствуют, но химические связи лежат на остальных ребрах.
График ромбического додекаэдра негамильтонов .
Ромбический додекаэдр можно разрезать на четыре тупых треугольных трапеции вокруг его центра. Эти ромбоэдры являются ячейками треугольных трапециевидных сот . Аналогия: правильный шестиугольник можно разрезать на 3 ромба вокруг его центра. Эти ромбы представляют собой плитки ромбика .
В коллекциях Лувра есть матрица в форме ромбического додекадрона, датируемая Птолемеевым Египтом . Грани начертаны греческими буквами, представляющими числа от 1 до 12: Α Β Γ Δ Ε Ζ Ϛ Η Θ Ι ΙΑ ΙΒ. Функция матрицы неизвестна.
Способ 2
Второй способ немного сложнее первого, так как чертеж придется изготавливать самостоятельно. Процесс происходит в несколько этапов:
- Чертим квадрат на листе бумаги.
- Выбираем одну из сторон и строим на ней правильный треугольник с равными сторонами. Для этого откладываем от двух углов, прилегающих к одной и той же стороне квадрата, по 60 градусов с помощью транспортира. На пересечении этих линий будет третья точка треугольника. Соединяем все три точки.
- Далее строим треугольники на каждой стороне квадрата.
- На одной стороне каждого треугольника оставляем припуски, которые помогут нам склеить фигуру.
- Таких чертежей вам необходимо изготовить два.
- Вырезаем каждый чертеж по контуру.
- Сгибаем треугольники вовнутрь, припуски промазываем клеем и склеиваем пирамиды.
- После того, как пирамиды подсохнут, смазываем квадратное дно клеем и соединяем две фигуры в одну.
- Оставляем октаэдр до полного высыхания.
- Октаэдром можно пользоваться, после того, как фигура полностью высохнет.
Низкополигональные миры
Наверное, все уже слышали о подобного рода иллюстрациях. В процессе создания объёмного 3D-изделия, она формируется при помощи полигонов. Чем их численность выше, тем реалистичнее будет вид. Раньше всегда ценилась высокая степень проработки изображений и мастера стремились к высокому числу полигонов, заготовки с низким числом были лишь набросками, считались незаконченной работой.


французская улица, кофейня и дама в шляпе

Для сборки сурового викинга с топором потребуется неделя усидчивости, не меньше.






Jeremiah Shaw
Пример того как можно сочетая два цвета (серый и зелёный) и три простые фигуры дерево, трава и камень создать низкополигональный шедевр, причем масштаб зависит только от вашего воображения и возможностей.

Интересные факты
Тетраэдр – одно из самых интересных, с точки зрения коммерции, платоновых тел. Достаточно простая пирамидка известна каждому с детства. В таких треугольных пакетах – тетропаках во времена СССР продавали молоко, кефир и сливки. Считалось, что благодаря пирамидальной форме деликатная продукция дольше сохраняется свежей.
Треугольная упаковка – совсем не советское изобретение. В 1930-х годах французский научно-популярный журнал «Science & Vie» опубликовал статью о загадочных свойствах египетских пирамид, где тела фараонов не портились, а мумифицировались естественным путём. Теория не подкреплялась серьёзными доказательствами, однако шведский изобретатель Эрик Валленберг настолько увлёкся ею, что создал мини-аналог древнеегипетских усыпальниц – ту самую картонную упаковку Tetra Classic. Он хотел снизить потери молокоторговцев, но на деле оказал помощь производителям одноразовой тары. Его пирамидки выпускались быстро, в больших объёмах и практически без отходов.

В 1950 году на базе инновационной технологии была создана компания AB Tetra Pak. Однако, когда выяснилось, что продукция в картонных пирамидках скисает почти так же быстро, как в стеклянных бутылках, шведы утратили интерес к идее Валленберга. Тем не менее, технологию производства удалось продать советскому руководству, делая упор на её бюджетность и эффективность. Так на наших прилавках появились легендарные «треугольнички» с надписью «Молоко». Чтобы транспортировка пакетов-тетраэдров была не менее выгодной, чем производство, под них изготовили специальные шестиугольные контейнеры.
Сегодня трёхмерные треугольные пакеты (точнее, пакетики) взяла на вооружение компания Lipton. Производитель утверждает, что заменяет плоскую порционную упаковку объёмной, чтобы продемонстрировать красоту раскрывшегося в чашке чайного листа. И показать, что в пакетиках не обрезки и крошка, как подозревают потребители, а полноценный качественный купаж.
Поделки из бумаги – увлечение на всю жизнь
Что-то делать руками всегда интересно и полезно, особенно если получается красиво. Ручная несложная работа помогает успокоить нервы после тяжелого трудового дня и развивает фантазию (особенно у детей). В Китае данный вид творчества известен как оригами, и давно с успехом помогает лечить душевнобольных людей и детишек, страдающими нервными заболеваниями. Такие занятия повсеместно применяются на уроках труда в школах или в старших группах в детских садах, что позволяет развить усидчивость, воображение и мелкую моторику, которая в свою очередь развивает умственную деятельность. Часто детские журналы предлагают схемы различных зверюшек, фигурок для совместной работы взрослых с детьми. Мы предлагаем схемы кубиков из бумаги или картона с различными вариантами картинок. Такие поделки будут интересны как малышам, так и школьникам, их можно преподнести в качестве подарка, сделанного своими руками. Взрослые так же могут использовать сделанные по нашим разверткам кубики, например кубик-календарь.
Пошаговая инструкция: как сделать куб из картона
1. Распечатайте необходимое количество шаблонов, например для кубика-календаря – необходимо оба варианта, а для кубиков с алфавитом – распечатайте столько, сколько нужно для складывания слов. 2. Аккуратно вырежьте схему куба. Вырезать удобнее ножницами, но можно воспользоваться и канцелярским ножом. 3. Согните вырезанный шаблон куба по линиям, чем аккуратнее вы согнёте схему куба, тем лучше будет смотреться ваше изделие. 4. Смажьте затемненные участки клеем и сторону за стороной соберите весь куб.
| Развертка простого куба (грань 5 см) | Развертка куба с арабскими цифрами 1,2,3,4,5,6 (грань — 5 см) | Развертка куба с арабскими цифрами 7,8,9,0,1,2 (грань — 5 см) |
| Развертка куба с римскими цифрами I, X, L, C, V, D (грань — 5 см) | Развертка куба с римскими цифрами I, M, V, X, ↁ, ↂ (грань — 5 см) | Куб с формулами (грань — 5 см) |
| Схема куба с английским алфавитом A, B, C, D, E, F (грань 6,5 см) | Схема куба с английским алфавитом G, H, I, J, K, L (грань 6,5 см) | Схема куба с английским алфавитом M, N, O, P, R, Q (грань 6,5 см) |
| Схема куба с английским алфавитом S, T, U, R, V, W (грань 6,5 см) | Схема куба с английским алфавитом X, Y, Z, A, B, C (грань 6,5 см) | Схема куба с русским алфавитом А, Б, В, Г, Д, Е (грань 6,5 см) |
| Схема куба с русским алфавитом Ж, З, И, Й, К, Л (грань 6,5 см) | Схема куба с русским алфавитом М, Н, О, П, Р, С (грань 6,5 см) | Схема куба с русским алфавитом У, Ф, Х, Ц, Ч, Т (грань 6,5 см) |
| Схема куба с русским алфавитом Ш, Э, Ъ, Ы, Ь, Щ (грань 6,5 см) | Схема куба с русским алфавитом Ю, Я, А, Б, В, Г (грань 6,5 см) | Схема куба с материками (грань 6,5 см) |
| Схема куба с портретами ученых |
И еще немного о кубиках из бумаги
Сейчас детские магазины переполнены всякими игрушками, в том числе и развивающими. Можно найти практически всё на любой возраст и кошелёк. Но иногда бывет трудно найти кубики, которые нам знакомы с детства. Кубики – это своего рода конструкторы, с которыми с удовольствием играют детишки. По рекомендациям педагогов, психологов и педиаторов малышам до 1 года уже можно давать игрушки-кубики. Они отлично развивают не только координацию, воображение, но при этом задействуют практически все мышцы рук, что прекрасно развивает мелкую моторику малыша. Из какого только материала не делают кубики – и из пластика, из дерева, из стекла, мы предлагаем вам сделать кубики из бумаги. Кубики с картинками с изображением цифр или букв будут прекрастным подспорьем для родителей и воспитателей в процессе подготовки ребёнка к школе. Более того, игра с кубиком даст малышу представление о геометрическх фигурах, в частности о кубе, о его свойствах. Если вы распечатаете и другие объемные геометрические фигуры (пирамиды, тетраэдр и т.д.), это значительно расширит кругозор ребёнка и поможет в процессе обучения в школе. Совместные занятия взрослых и детей очень сближают и укрепляют семью.
Сейчас практически в каждом доме есть компьютер и принтер, т.е. ваши затраты – это стоимость бумаги, формата А4. Приведённые на данной странице шаблоны куба можно редактировать, т.е. взяв чистую развёртку куба, вы можете смело вставлять свои картинки и распечатать новый вариант. В качестве картинок можно взять рисунки или фотографии зверей, животных, машин, а так же фотографии знаменитостей или своих родственников, полет фантазии безграничен. Успехов вам в творчестве и в воспитании!
Развертка и схема куба из бумаги
| Разноцветный куб 1 (грань 6,5 см) | Разноцветный куб 2 (грань 6,5 см) | Игральный куб (грань 5 см) |
| Куб-календарь на 2013 год (январь-июнь, грань 6,5 см) | Куб-календарь на 2013 год (июль-декабрь,грань 6,5 см) |
Григорий Андреев
Изучаем простых бумажных животных: как сделать фигурки своими руками
Предлагаем вам научиться делать элементарные и оригинальные фигурки животных из бумажных листов. Для начинающих рукодельниц такие схемы и описания очень простые и доступные в исполнении.
Из простого бумажного листа можно сделать смешную и забавную фигурку собаки. Возьмите лист бумаги квадратной формы и загните его верхние углы. Затем необходимо сложить лист по диагональному направлению широкой стороной наверх. Далее следует загнуть верхние острые концы по направлению вперед и вниз. Это будут уши вашей бумажной собаки. Теперь уголок, который образовался в результате данных мероприятий вам необходимо загнуть назад.
Далее на мордочке животного вам необходимо нарисовать глаза и нос вашей собачки. Для более наглядного и понятного восприятия процесса изготовления бумажного животного можете посмотреть несколько схем, представленных на фото ниже.
Ели же вы завернете уголки, расположенные сверху, не по направлению вперед, а назад, то вы сможете сделать фигурку кота.
Еще проще и быстрее можно сформировать нежные и завораживающие фигурки певчих птичек из бумажного материала. Подберите красивую декоративную бумагу с красочным принтом и нарисуйте или поищите в Интернете желаемый шаблон птички.
Из декоративной бумажной материи контрастного оттенка необходимо вырезать крыло птички, которое затем прикрепить на основу птицы, вырезанную из бумаги. Теперь проденьте декоративный шнур через отверстие красочной пуговицы и завяжите красивым бантиком. Далее приклейте при помощи крепкого клея на заготовку пуговицу с декоративным бантиком.
При помощи дырокола из листа бумаги сделайте кружочки для формирования глаз птички. Осталось приклеить их на правильное место. Ваша бумажная певчая птичка готова.
Для того чтобы выполнить такую простую и оригинальную композицию из бумажного материала, понадобятся лист цветной бумаги красного оттенка и лист бумаги зеленого цвета.
Сначала бумажную заготовку в виде квадрата со сторонами восемь с половиной сантиметров, вырезанную из листа бумаги красного оттенка, необходимо два раза сложить по диагональному направлению. Затем левую сторону и правую сторону квадрата следует согнуть внутрь. Далее вам необходимо обрезать уголки таким образом, чтобы туловище божьей коровки приобрело овальную форму. Для завершения бумажной оригинальной поделки, туловище божьей коровки необходимо разрисовать и приклеить фигурку на лист бумаги зеленого цветового оттенка. Теперь ваша объемная композиция завершена.
Пошаговый туториал
Нарисуйте вспомогательные линии, точка пересечения будет центром нашего октаэдра.
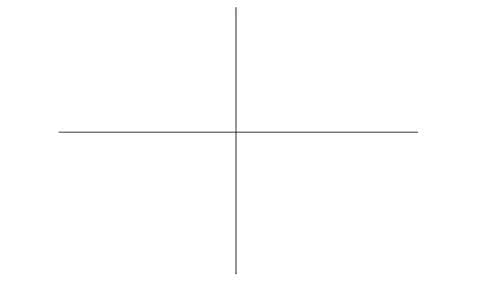
Шаг 2
Нарисуйте круг с центром в точке пересечения вспомогательных линий. Стоит сказать, что октаэдр является геометрической фигурой, которую можно вписать в шар таким образом, что каждая вершина октаэдра будет иметь общую точку с поверхностью шара. Но так как мы рисуем октаэдр в двумерном пространстве, мы нарисуем круг.
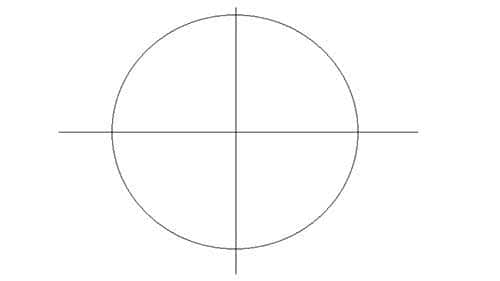
Шаг 3
Нарисуйте эллипс. Если представить его в трёхмерном виде, то это будет горизонтальная плоскость разделяющая шар на две равных полусферы.
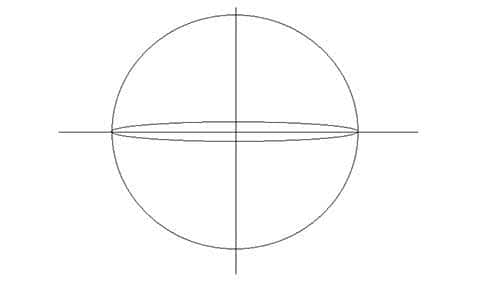
Шаг 4
Нарисуйте параллелограмм, так чтобы две его вершины совпадали с точками пересечения круга и горизонтальной линии, а две другие располагались на эллипсе.
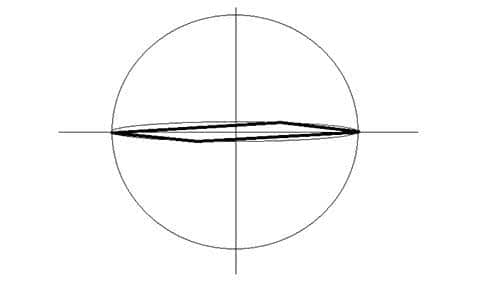
Соедините каждую вершину параллелограмма с точкой пересечения круга и вертикальной линией.
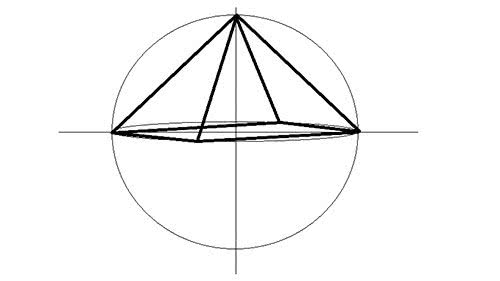
Шаг 6
Аналогично соедините линии в нижней части фигуры и ваш октаэдр будет готов. По желанию можете стереть все вспомогательные линии, а так же те линии, которые не должны быть видны, если вы хотите получить не прозрачный октаэдр.
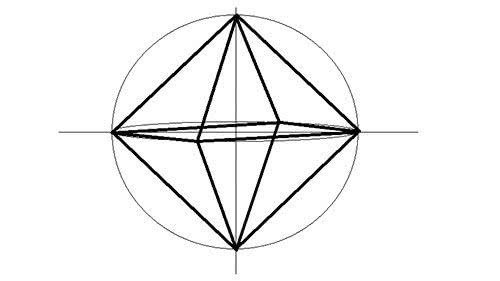
Источник
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
- Выбираем размеры пирамиды и количество ее граней.
- Рисуем основание — многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
- От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее. Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
- Вырезаем и склеиваем фигуру.
- Пирамида готова!
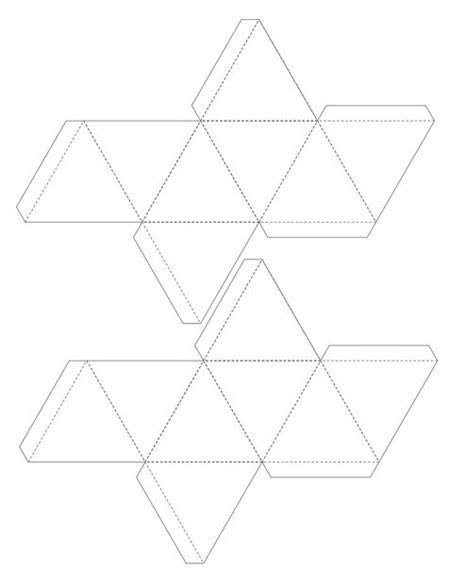
Источник